विषयसम्मिश्र संख्याएं और बहुपद

भाषण 22

§एक। जटिल संख्याएँ: मूल परिभाषाएँ

चिन्ह, प्रतीक अनुपात दर्ज करें
और काल्पनिक इकाई कहलाती है। दूसरे शब्दों में,
.

परिभाषा। फॉर्म की अभिव्यक्ति
, कहाँ पे
, को सम्मिश्र संख्या कहा जाता है, और संख्या सम्मिश्र संख्या का वास्तविक भाग कहलाता है और निरूपित करें
, संख्या - काल्पनिक भाग और निरूपित करें
.

इस परिभाषा से यह निष्कर्ष निकलता है कि वास्तविक संख्याएँ वे सम्मिश्र संख्याएँ होती हैं जिनका काल्पनिक भाग शून्य के बराबर होता है।

एक समतल के बिंदुओं के रूप में सम्मिश्र संख्याओं को निरूपित करना सुविधाजनक है, जिस पर एक कार्तीय आयताकार समन्वय प्रणाली दी गई है, अर्थात्: एक सम्मिश्र संख्या
बराबर अंक
और इसके विपरीत। धुरी पर
वास्तविक संख्याएँ प्रदर्शित होती हैं और इसे वास्तविक अक्ष कहते हैं। फॉर्म की जटिल संख्या

विशुद्ध रूप से काल्पनिक कहा जाता है। उन्हें अक्ष पर डॉट्स के रूप में दिखाया गया है।
, जिसे काल्पनिक अक्ष कहा जाता है। यह तल, जो सम्मिश्र संख्याओं को निरूपित करने का कार्य करता है, सम्मिश्र तल कहलाता है। एक सम्मिश्र संख्या जो वास्तविक नहीं है, अर्थात्। ऐसा है कि
, जिसे कभी-कभी काल्पनिक कहा जाता है।

दो सम्मिश्र संख्याओं को समान कहा जाता है यदि और केवल यदि उनके वास्तविक और काल्पनिक भाग समान हों।

जटिल संख्याओं का जोड़, घटाव और गुणा बहुपद बीजगणित के सामान्य नियमों के अनुसार किया जाता है, इस तथ्य को ध्यान में रखते हुए कि

. विभाजन संक्रिया को गुणन संक्रिया के व्युत्क्रम के रूप में परिभाषित किया जा सकता है और कोई भी परिणाम की विशिष्टता साबित कर सकता है (यदि भाजक शून्य से भिन्न है)। हालांकि, व्यवहार में, एक अलग दृष्टिकोण का उपयोग किया जाता है।

जटिल आंकड़े
तथा
संयुग्म कहलाते हैं, जटिल तल पर उन्हें वास्तविक अक्ष के बारे में सममित बिंदुओं द्वारा दर्शाया जाता है। यह स्पष्ट है कि:

1)

;

2)
;

3)
.

अब विभाजित पर निम्नानुसार किया जा सकता है:

.

यह दिखाना मुश्किल नहीं है कि

,

जहां प्रतीक किसी भी अंकगणितीय ऑपरेशन के लिए खड़ा है।

होने देना
कुछ काल्पनिक संख्या, और एक वास्तविक चर है। दो द्विपदों का गुणनफल

वास्तविक गुणांकों वाला एक वर्ग त्रिपद है।

अब, हमारे पास सम्मिश्र संख्याएँ होने के कारण, हम किसी भी द्विघात समीकरण को हल कर सकते हैं
।तो अगर

और समीकरण के दो जटिल संयुग्मी मूल हैं

.

यदि एक
, तो समीकरण के दो भिन्न वास्तविक मूल हैं। यदि एक
, तो समीकरण के दो समान मूल हैं।

2. एक सम्मिश्र संख्या का त्रिकोणमितीय रूप

जैसा कि ऊपर बताया गया है, सम्मिश्र संख्या
एक बिंदु के साथ प्रतिनिधित्व करने के लिए सुविधाजनक
. इस बिंदु के त्रिज्या वेक्टर के साथ ऐसी संख्या की पहचान भी की जा सकती है
. इस व्याख्या के साथ, जटिल संख्याओं का जोड़ और घटाव वैक्टर के जोड़ और घटाव के नियमों के अनुसार किया जाता है। सम्मिश्र संख्याओं के गुणन और विभाजन के लिए, दूसरा रूप अधिक सुविधाजनक है।

हम जटिल विमान पर परिचय देते हैं
ध्रुवीय समन्वय प्रणाली। फिर कहाँ
,
और सम्मिश्र संख्या
के रूप में लिखा जा सकता है:

संकेतन के इस रूप को त्रिकोणमितीय कहा जाता है (बीजीय रूप के विपरीत
) इस रूप में, संख्या मॉड्यूल कहा जाता है और - जटिल संख्या तर्क . वे चिह्नित हैं:
,

. मॉड्यूल के लिए, हमारे पास सूत्र है

संख्या तर्क अस्पष्ट रूप से परिभाषित किया गया है, लेकिन एक शब्द तक
,
. तर्क का मूल्य जो असमानताओं को संतुष्ट करता है
, प्रिंसिपल कहा जाता है और निरूपित
. फिर,
. तर्क के मुख्य मूल्य के लिए, आप निम्नलिखित भाव प्राप्त कर सकते हैं:

,

संख्या तर्क
अपरिभाषित माना जाता है।

त्रिकोणमितीय रूप में दो जटिल संख्याओं की समानता की शर्त का रूप है: संख्याओं के मॉड्यूल समान हैं, और तर्क एक से अधिक भिन्न हैं
.

त्रिकोणमितीय रूप में दो सम्मिश्र संख्याओं का गुणनफल ज्ञात कीजिए:

इसलिए, संख्याओं को गुणा करते समय, उनके मॉड्यूल गुणा किए जाते हैं, और तर्क जोड़े जाते हैं।

इसी तरह, यह स्थापित किया जा सकता है कि विभाजित करते समय, संख्याओं के मॉड्यूल विभाजित होते हैं, और तर्क घटाए जाते हैं।

घातांक को कई गुणा के रूप में समझते हुए, हम एक जटिल संख्या को एक घात तक बढ़ाने का सूत्र प्राप्त कर सकते हैं:

हम के लिए एक सूत्र प्राप्त करते हैं
- जड़ एक सम्मिश्र संख्या की शक्ति (वास्तविक संख्या के अंकगणितीय मूल के साथ भ्रमित होने की नहीं!) रूट एक्सट्रैक्शन ऑपरेशन एक्सपोनेंटिएशन ऑपरेशन का विलोम है। इसीलिए
एक सम्मिश्र संख्या है ऐसा है कि
.

होने देना
ज्ञात, और
पाया जाना आवश्यक है। फिर

त्रिकोणमितीय रूप में दो सम्मिश्र संख्याओं की समानता से, यह इस प्रकार है कि

,
,
.

यहाँ से
(यह एक अंकगणितीय जड़ है!),

,
.

यह सत्यापित करना आसान है कि केवल स्वीकार कर सकते हैं अनिवार्य रूप से भिन्न मान, उदाहरण के लिए, जब
. अंत में हमारे पास सूत्र है:

,
.

तो जड़ एक सम्मिश्र संख्या से th डिग्री है विभिन्न मूल्य। जटिल तल पर, ये मान सही ढंग से कोने पर स्थित होते हैं -गोन त्रिज्या के एक वृत्त में खुदा हुआ
मूल पर केंद्रित। "पहले" रूट में एक तर्क है
, दो "पड़ोसी" जड़ों के तर्क अलग-अलग हैं
.

उदाहरण। आइए काल्पनिक इकाई का घनमूल लें:
,
,
. फिर:

,

वैज्ञानिक और व्यावहारिक सम्मेलन

"विज्ञान में पहला कदम"

खंड" गणित"

पूरा हुआ: 9वीं कक्षा के छात्र एमबीओयू

"मोर्दोवियन-पेवस्काया माध्यमिक विद्यालय"

एरोचिन इवान

पर्यवेक्षक:गणित शिक्षक

कदिशकिना एन.वी.

इंसार 2014

विषयसूची

परिचय…………………………………………………………………

सम्मिश्र संख्याओं की खोज का इतिहास ………………………… 4

2.1. सम्मिश्र संख्याओं के बारे में महान वैज्ञानिकों की बातें…. चार

2.2 सम्मिश्र संख्याओं के उद्भव पर………………………………4

मुख्य हिस्सा

सम्मिश्र संख्याओं की परिभाषा………………………. आठ

2.1. एक सम्मिश्र संख्या का बीजगणितीय रूप………………8

2.2. सम्मिश्र संख्याओं पर संक्रियाएँ……………………9

3. एक जटिल चर के साथ समीकरणों को हल करना ……………… 12

4. जटिल तल की अवधारणा……………………………….. 14

5. एक सम्मिश्र संख्या का ज्यामितीय रूप…………………….. 15

6. संख्या का त्रिकोणमितीय रूप………………………………….. 17

7. एक सम्मिश्र संख्या के घात को बढ़ाना………………………. 19

संख्या का घातीय रूप ……………………………………… 20

सम्मिश्र संख्याओं का प्रयोग कहाँ होता है? .. 21

निष्कर्ष। निष्कर्ष……………………………………………… 23

सन्दर्भ …………………………………………… 24

"कॉम्प्लेक्स नंबर्स" विषय पर टेस्ट ………………………। 25

परिचय प्राचीन काल में, गिनती करना सीखकर, लोगों ने मात्रा का माप - संख्या सीखा। NUMBER - गणित की मूल अवधारणाओं में से एक, प्राचीन काल में उत्पन्न हुई और धीरे-धीरे विस्तारित और सामान्यीकृत हुई। प्राकृतिक सुंदरता से आकर्षक, आंतरिक सद्भाव से भरा, सुलभ, लेकिन फिर भी समझ से बाहर, प्रतीत होने वाली सादगी के पीछे कई रहस्य छुपाता है ... हमारे जीवन में, हम में से प्रत्येक संख्या के साथ ढेर होता है। उनके बिना स्कूली पाठ्यक्रम और आगे के जीवन की कल्पना करना कठिन है।

प्राकृतिक, संपूर्ण, तर्कसंगत, तर्कहीन, वास्तविक। वे मुझे हर साल अधिक से अधिक आकर्षित करते हैं। पिछले साल, मैंने रहस्यमय संख्या पीआई पर शोध किया था। मुझे जटिल संख्याओं में दिलचस्पी थी। मैंने पहली बार उनके बारे में 8वीं कक्षा में द्विघात समीकरणों को हल करते हुए सुना था। 9वीं कक्षा में, मुझे घन समीकरणों को हल करने में गंभीर समस्याएं थीं, जिनकी तीन जड़ें होनी चाहिए, क्योंकि एक बहुपद को रैखिक कारकों में विघटित करने के बाद, द्विघात समीकरण को हल करना आवश्यक हो जाता है। और अचानक यह पता चला कि विवेचक ऋणात्मक है, अर्थात द्विघात समीकरण की कोई जड़ें नहीं हैं, क्योंकि द्विघात समीकरण की जड़ों को खोजने पर, मुझे अंकगणितीय वर्गमूल को ऋणात्मक संख्या से निकालने की आवश्यकता होती है। और इसका मतलब है कि तीन जड़ों के बजाय घन समीकरण में केवल एक जड़ है। इस तरह मुझे विरोधाभास मिला। और मैंने इसे देखने का फैसला किया। वास्तविक संख्याओं के सेट पर ऐसा ऑपरेशन असंभव है, लेकिन असंभव बिल्कुल नहीं है। यह पता चला कि मैं जिस समीकरण को हल कर रहा था उसकी जड़ें जटिल संख्याओं के समूह से संबंधित हैं, जिसमें एक संख्या होती है जिसका वर्ग -1 होता है।जब मैंने सम्मिश्र संख्याओं के बारे में बहुत कुछ सीखा तो मेरी रुचि और भी बढ़ गई।

उद्देश्य:गणित की एक शाखा के रूप में सम्मिश्र संख्याओं का अध्ययन करना और गणित की कई शाखाओं में उनकी भूमिका का अध्ययन करना।

अनुसंधान के उद्देश्य:

1. इस मुद्दे पर साहित्य का विश्लेषण करें;

2. संख्याओं के बारे में जानकारी व्यवस्थित करें;

3. एक तरह से प्राकृतिक से जटिल तक संख्या सेट का विस्तार करें

एक नए गणितीय उपकरण का निर्माण।

4. बीजीय परिवर्तन की तकनीक में सुधार।

5. 9वीं कक्षा के छात्रों द्वारा जटिल संख्याओं के अध्ययन में उनकी रचनात्मक और शोध क्षमताओं को विकसित करने में रुचि बढ़ाने में, गणित में जटिल संख्याओं के महत्व और भूमिका का आकलन करें।

संकट:बीजगणित के पाठ्यक्रम के लिए कार्यक्रमों में अनुपस्थिति और जटिल संख्याओं का अध्ययन करने वाले अनुभाग के सामान्य शैक्षणिक संस्थानों के लिए विश्लेषण की शुरुआत।

कार्य परिकल्पना:यह माना जाता है कि छात्रों द्वारा जटिल संख्याओं का परिचय और अध्ययन उन्हें गणित के कई वर्गों में अपने ज्ञान को गहरा करने की अनुमति देगा, उन्हें विभिन्न समस्याओं को हल करने के लिए एक अतिरिक्त उपकरण से लैस करेगा।

अध्ययन का विषय:जटिल आंकड़े।

अध्ययन की वस्तु: एक सम्मिश्र संख्या और उन पर क्रियाओं को निर्दिष्ट करने के लिए प्रपत्र।

अनुसंधान की विधियां:

1. साहित्यिक स्रोतों का अध्ययन और विश्लेषण।

2. व्यावहारिक समस्याओं का समाधान

3. एक परीक्षण विकसित करें।

4. साक्षात्कार।

5. किए गए कार्य का विश्लेषण।

विषय की प्रासंगिकता।

मुझे लगता है कि मेरा विषयसे मिलता जुलता , चूंकि हमारे समय में बहुत सारे वैज्ञानिक और शैक्षिक साहित्य हैं, लेकिन सभी प्रकाशनों में सामग्री स्पष्ट रूप से, समझने योग्य और हम छात्रों के लिए सुलभ नहीं है। जब मैंने सम्मिश्र संख्याओं के बारे में बहुत कुछ सीखा तो मेरी रुचि और भी बढ़ गई। यहाँ इस विषय पर मेरे काम का परिणाम है।

मुख्य हिस्सा।

सम्मिश्र संख्याओं की खोज का इतिहास

1. जटिल संख्याओं के बारे में प्रसिद्ध वैज्ञानिकों की कुछ बातें:

काल्पनिक संख्याएँ दिव्य आत्मा की एक सुंदर और अद्भुत शरणस्थली हैं। लगभग शून्य के साथ एक उभयचर। जी. लिबनिज़ो

“इसके अलावा और यहां तक ​​कि इस या उस गणितज्ञ की इच्छा के विरुद्ध, काल्पनिक संख्याएँ गणना में बार-बार दिखाई देती हैं, और केवल धीरे-धीरे, जैसे ही उनके उपयोग के लाभ खोजे जाते हैं, क्या वे अधिक से अधिक व्यापक हो जाते हैं ”एफ। क्लेन।

आखिरकार, कोई भी काल्पनिक मात्राओं के साथ गणना में प्राप्त परिणामों की सटीकता पर संदेह नहीं करता है, हालांकि वे केवल बीजगणितीय रूप और हास्यास्पद मात्रा के चित्रलिपि हैं।

एल. कार्नो

1. जटिल संख्याओं का उद्भव।

संख्या की अवधारणा को प्राकृतिक से वास्तविक तक विस्तारित करने की प्रक्रिया अभ्यास की आवश्यकताओं और स्वयं गणित की आवश्यकताओं दोनों से जुड़ी हुई थी। प्राचीन यूनानी वैज्ञानिक केवल प्राकृतिक संख्याओं को "वास्तविक" मानते थे, लेकिन व्यावहारिक गणना में दो सहस्राब्दी ईसा पूर्व के लिए। प्राचीन बाबुल और प्राचीन मिस्र में पहले से ही अंशों का उपयोग किया जाता था। संख्या की अवधारणा के विकास में अगला महत्वपूर्ण चरण नकारात्मक मूल्यों की उपस्थिति था। उन्हें दो शताब्दी ईसा पूर्व चीनी वैज्ञानिकों द्वारा पेश किया गया था। ई।, और प्राचीन यूनानी गणितज्ञडायोफैंटस इन तृतीय शताब्दी ई इ। पहले से ही जानता था कि नकारात्मक पर कार्रवाई कैसे करेंठोस संख्या।

गणित में इन्हें वास्तविक संख्याओं का समुच्चय कहा जाता है।

सभी वास्तविक संख्याएँ संख्या रेखा पर स्थित होती हैं:

वास्तविक संख्याओं का संघ बहुत रंगीन है - यहाँ पूर्ण संख्याएँ, और भिन्न, अपरिमेय संख्याएँ हैं। इस मामले में, प्रत्येक संख्यात्मक बिंदु आवश्यक रूप से कुछ वास्तविक संख्या से मेल खाता है।

पर तेरहवें सदी ने वर्गमूल निकालना शुरू कियासकारात्मक संख्याओं से और पाया कि संख्याओं के साथ ऋणात्मकयह ऑपरेशन संभव नहीं है। लेकीन मेXVI अध्ययन के सिलसिले में सदीगणित के घन समीकरणों में एक समस्या आई:घन समीकरणों के अध्ययन के संबंध में, ऋणात्मक संख्याओं से वर्गमूल निकालना आवश्यक हो गया।

परसंरेखण ज़रूरीनामहोनातीन जड़ें. इसे हल करते समय, अक्सरवर्गमूल चिह्न के नीचे एक ऋणात्मक संख्या दिखाई दी। यह पता चला कि इन जड़ों का मार्ग ऋणात्मक संख्या के वर्गमूल को निकालने के असंभव संचालन से होकर जाता है।

परिणामी विरोधाभास की व्याख्या करने के लिए, 1545 में इतालवी बीजगणित गिरोलामो कार्डानो ने एक नई प्रकृति की संख्याओं को पेश करने का प्रस्ताव रखा। उन्होंने दिखाया कि समीकरणों की प्रणाली x + y = 10, xy = 40 जिसका वास्तविक संख्याओं के समुच्चय में कोई हल नहीं है, हमेशा एक हल होता है x = 5 ±
, वाई = 5 ±
, हमें केवल साधारण बीजगणित के नियमों के अनुसार ऐसे भावों पर कार्य करने के लिए सहमत होने की आवश्यकता है और मान लें कि
∙
= - एक। कार्डानो ने ऐसी मात्राओं को "शुद्ध" कहा नकारात्मक" और यहां तक ​​कि "परिष्कृत रूप से नकारात्मक",लेकिन उसने उन्हें पूरी तरह से बेकार माना और उनका इस्तेमाल न करने का प्रयास किया। हालाँकि, पहले से ही 1572 में, उनके हमवतन आर। बॉम्बेली ने एक पुस्तक प्रकाशित की, जिसमें ऐसी संख्याओं पर अंकगणितीय संक्रियाओं के लिए पहले नियम स्थापित किए गए थे, जिसमें से निष्कर्षण तकउन्हें घन जड़ें।

"काल्पनिक संख्या" नाम 1637 . में पेश किया गया था

फ्रांसीसी गणितज्ञ और दार्शनिक आर. डेसकार्टेस।

और 1777 में सबसे महान बीजगणितविदों में से एक XVIII सेंचुरी - एल। यूलर - ने फ्रांसीसी शब्द . के पहले अक्षर का उपयोग करने का सुझाव दियाकल्पना (सोच my) एक संख्या को दर्शाने के लिएमैं =
.

यह प्रतीक के. गॉस की बदौलत सामान्य उपयोग में आया।शब्द "जटिल आंकड़े 1831 में गॉस द्वारा भी पेश किया गया था। जटिल शब्द (लैटिन सेपरिसर ) का अर्थ है कनेक्शन, संयोजन, अवधारणाओं का सेट, वस्तुएं, घटना, आदि।, के बारे में एक पूरे का गठन।

XVII के दौरान सदी ने काल्पनिक संख्याओं की अंकगणितीय प्रकृति की चर्चा जारी रखी, उन्हें एक ज्यामितीय औचित्य देने की संभावना।

सम्मिश्र संख्याओं पर संक्रियाओं की तकनीक धीरे-धीरे विकसित हुई। किनारे पर XVII - XVIII सदियों, जड़ों का एक सामान्य सिद्धांत बनाया गया थाएन वें डिग्री, पहले नकारात्मक से, और बाद में किसी भी जटिल संख्या से।

XVIII के अंत में सदी में, फ्रांसीसी गणितज्ञ जे. लैग्रेंज यह कहने में सक्षम थे कि काल्पनिक मात्राएँ अब गणितीय विश्लेषण को जटिल नहीं बनाती हैं। सम्मिश्र संख्याओं की सहायता से उन्होंने अचर गुणांक वाले रैखिक अवकल समीकरणों के हलों को व्यक्त करना सीखा। इस तरह के समीकरणों का सामना करना पड़ता है, उदाहरण के लिए, एक प्रतिरोधी माध्यम में भौतिक बिंदु के दोलनों के सिद्धांत में।

जे. बर्नौली ने समाकलों की गणना के लिए सम्मिश्र संख्याओं का प्रयोग किया। हालांकि इस दौरान XVIII सदी, जटिल संख्याओं की मदद से, कार्टोग्राफी, हाइड्रोडायनामिक्स आदि से संबंधित लागू समस्याओं सहित कई मुद्दों को हल किया गया था, लेकिन इन संख्याओं के सिद्धांत के लिए अभी भी कोई कठोर तर्क नहीं था। इसलिए, फ्रांसीसी वैज्ञानिक पी. लाप्लास का मानना ​​था कि काल्पनिक संख्याओं की सहायता से प्राप्त परिणाम केवल मार्गदर्शन हैं, प्रत्यक्ष प्रमाण द्वारा पुष्टि के बाद ही वास्तविक सत्य के चरित्र को प्राप्त करना। अंततः XVIII - प्रारंभिक XIX सदियों से, जटिल संख्याओं की एक ज्यामितीय व्याख्या प्राप्त की गई थी। डेन जी। वेसल, फ्रांसीसी जे। आर्गन और जर्मन के। गॉस ने स्वतंत्र रूप से जटिल संख्या का प्रतिनिधित्व करने का प्रस्ताव रखाजेड \u003d ए + द्वि बिंदु एम (ए, बी ) समन्वय तल पर। बाद में यह पता चला कि बिंदु M द्वारा नहीं, बल्कि मूल से इस बिंदु पर जाने वाले वेक्टर OM द्वारा संख्या का प्रतिनिधित्व करना और भी सुविधाजनक था। इस व्याख्या के साथ, जटिल संख्याओं का जोड़ और घटाव वैक्टर पर समान संचालन के अनुरूप होता है।

जटिल संख्याओं की ज्यामितीय व्याख्याओं ने एक जटिल चर के कार्यों से संबंधित कई अवधारणाओं को परिभाषित करना संभव बना दिया और उनके आवेदन के दायरे का विस्तार किया। यह स्पष्ट हो गया कि जटिल संख्याएं कई मुद्दों में उपयोगी होती हैं जहां वे एक विमान पर वैक्टर द्वारा दर्शायी जाने वाली मात्राओं से निपटते हैं: द्रव प्रवाह के अध्ययन में, लोच के सिद्धांत में समस्याएं, सैद्धांतिक विद्युत इंजीनियरिंग में।

एक जटिल चर के कार्यों के सिद्धांत के विकास में एक महान योगदान रूसी और सोवियत वैज्ञानिकों द्वारा किया गया था: आर.आई. मुस्केलिशविली लोच के सिद्धांत के लिए अपने अनुप्रयोगों में लगा हुआ था, एम.वी. केल्डिश और एम.ए. Lavrentiev - वायुगतिकी और जलगतिकी के लिए, N.N. Bogolyubov और V.S. व्लादिमीरोव - क्वांटम फील्ड थ्योरी की समस्याओं के लिए।

सम्मिश्र संख्याओं की परिभाषा

3.1 सम्मिश्र संख्या का बीजीय रूप

जटिल संख्या जेड अभिव्यक्ति कहा जाता है जेड = एक + बी मैं, कहाँ पे एक तथा बी वास्तविक संख्याएँ हैं,मैं 2 = -1,

एक = पुनः जेड – असली हिस्सा जेड (वास्तविक) (रे, फ्रेंच रे एली से - "वास्तविक", "वैध");

बी = मैं हूँ जेड काल्पनिक हिस्सा जेड (इम, फ्रांसीसी कल्पना से - "काल्पनिक") .

बी – एक सम्मिश्र संख्या के काल्पनिक भाग का गुणांक।

एक सम्मिश्र संख्या लिखना z एक + ib . के रूप में सम्मिश्र संख्या का बीजगणितीय रूप कहलाता है।

यदि एक एक 0, में 0, वह संख्या जेड- काल्पनिक ( जेड = 37 - 6 आई ).

ई अगर एक = 0 , में 0, वह संख्या जेड एक शुद्ध काल्पनिक संख्या है ( जेड = 22 मैं) .

यदि एक एक 0, पर = 0, जेड एक वास्तविक संख्या है ( जेड = -5).

मैं की शक्तियां:

मैं 1 = मैं
मैं 4एन+1 = मैं;

मैं 2 = - 1
मैं 4एन+2 = - 1;

मैं 3 = मैं 2 मैं
मैं 4n+3 = - मैं

मैं 4 = (मैं 2 ) 2 = 1
मैं 4 एन = 1।

यह सूत्रों से निम्नानुसार है कि बहुपद के साथ संचालन के नियमों के अनुसार जोड़ और गुणा किया जा सकता है, यह मानते हुए मैं 2 = -1। सम्मिश्र संख्याओं के जोड़ और गुणा की संक्रियाओं में वास्तविक संख्याओं के गुण होते हैं। बुनियादी गुण:

संपत्ति हस्तांतरण:

जेड 1 + जेड 2 \u003d जेड 2 + जेड 1, जेड 1 जेड 2 \u003d जेड 2 जेड 1

संबंधी संपत्ति:

(जेड 1 + जेड 2) + जेड 3 \u003d जेड 1 + (जेड 2 + जेड 3), (जेड 1 जेड 2) जेड 3 \u003d जेड 1 (जेड 2 जेड 3)

वितरण संपत्ति:

जेड 1 (जेड 2 + जेड 3) \u003d जेड 1 जेड 2 + जेड 1 जेड 3

दो विपरीत संख्याओं का योग 0 है (जेड + (- जेड ) = 0)

एक सम्मिश्र संख्या शून्य के बराबर होती है यदि वास्तविक और काल्पनिक भाग क्रमशः शून्य के बराबर हों।

3.2 सम्मिश्र संख्याओं पर संचालन.

बीजगणितीय रूप में लिखी गई सम्मिश्र संख्याओं के ऊपर, सभी अंकगणितीय संक्रियाओं को साधारण द्विपदों की तरह करना संभव है, केवल इस बात को ध्यान में रखते हुए मैं 2 = -1.

सम्मिश्र संख्याओं का जोड़ और घटाव।

सम्मिश्र संख्याओं का योग z 1 \u003d a 1 + b 1 i और z 2 \u003d a 2 - b 2 i के बराबर है:
जेड 1 + जेड 2 \u003d (ए 1 + ए 2) + (बी 1 + बी 2) आई

उदाहरण 1

दो सम्मिश्र संख्याएँ जोड़ेंजेड 1 = 1 +3 मैं, जेड 2 =4-5 मैं

दो सम्मिश्र संख्याओं को जोड़ने के लिए, उनके वास्तविक और काल्पनिक भागों को जोड़ें:

जेड 1 + जेड 2 \u003d 1 + 3i + 4 -5i \u003d 5 -2i

परिसर का अंतर जेड 1 = एक 1 + बी 1 मैं तथा जेड 2 = एक 2 – बी 2 मैं संख्या बराबर पर:

जेड 1 - जेड 2 \u003d (ए 1 - ए 2) + (बी 1 - बी 2) आई

उदाहरण 2

सम्मिश्र संख्याओं के अंतर ज्ञात कीजिएजेड 1 = -2 + मैंतथाजेड 2 = 4 मैं -2

कार्रवाई जोड़ के समान है, एकमात्र विशेषता यह है कि सबट्रेंड को कोष्ठक में लिया जाना चाहिए, और फिर, एक मानक के रूप में, इन कोष्ठकों को एक संकेत परिवर्तन के साथ खोलें:

z 1 - z 2 \u003d (-2 + i) - (4i - 2) \u003d -2 + I - 4i +2 \u003d - 3i

सम्मिश्र संख्याओं का गुणन

सम्मिश्र संख्याओं का गुणनफल z 1 \u003d a 1 + b 1 i और z 2 \u003d a 2 - b 2 i के बराबर है:

जेड 1 जेड 2 \u003d (ए 1 ए 2 - बी 1 बी 2) + (ए 2 बी 1 + बी 2 ए 1) मैं

उदाहरण 3सम्मिश्र संख्याओं का गुणनफल ज्ञात कीजिए

जेड 1 \u003d 1 - आई, जेड 2 \u003d 3 + 6i

z 1 z 2 \u003d (1 -i) (3 + 6i) \u003d 1 3 -i 3 + 1 6i - i 6i \u003d 3- 3i + 6i +6 \u003d 9 + 3i

सम्मिश्र संख्याओं का विभाजन

सम्मिश्र संख्याओं का भागफल जेड 1 = एक 1 + बी 1 · मैं तथा जेड 2 = एक 2 – बी 2 · मैं बराबर:

उदाहरण 4. मान लीजिए z 1 \u003d 13 + i, z 2 \u003d 7 - 6 i

भागफल ज्ञात करने के लिए, पहले भिन्न के अंश और हर को हर के संयुग्म से गुणा करें, और फिर शेष संक्रियाएँ करें।

सम्मिश्र संख्याओं से जड़ों का निष्कर्षण।

जड़ नहीं निकाल सकते? अगर हम वास्तविक संख्याओं के बारे में बात कर रहे हैं, तो यह वास्तव में असंभव है। जटिल संख्याओं में, आप जड़ निकाल सकते हैं - आप कर सकते हैं! ज्यादा ठीक, दोजड़:

क्या पाए गए मूल वास्तव में समीकरण का हल हैं? चलो देखते है:

इन जड़ों को भी कहा जाता है जटिल जड़ों को संयुग्मित करें.

ऋणात्मक संख्याओं से वर्गमूल निकालने पर, हमें प्राप्त होता है दोजटिल जड़ों को संयुग्मित करें।

उदाहरण के लिए, , , , ,

एक जटिल चर के साथ समीकरणों को हल करना

सबसे पहले, मैंने सबसे सरल द्विघात समीकरण पर विचार किया z 2 = a , जहाँ a - एक दी गई संख्या,जेड अज्ञात है। वास्तविक संख्याओं के समुच्चय पर, यह समीकरण है:

1) एक जड़ हैजेड = 0 अगर ए = 0;

2) के दो वास्तविक मूल हैंजेड 1,2 = ±
अगर एक> 0;

3) का कोई वास्तविक मूल नहीं है यदिएक< 0;

4) सम्मिश्र संख्याओं के समुच्चय पर, इस समीकरण का हमेशा एक मूल होता है।

सामान्य तौर पर, समीकरण z 2 = a , जहाँ a < 0 имеет два комплексных корня: जेड 1,2 = ±
मैं ।

समानता का उपयोग करनामैं 2 = -1, ऋणात्मक संख्याओं के वर्गमूल आमतौर पर इस प्रकार लिखे जाते हैं:
= मैं,
= मैं
= 2 मैं,
= मैं
.

इसलिए,
किसी भी वास्तविक संख्या के लिए परिभाषितएक (सकारात्मक, नकारात्मक और शून्य)। तो कोई द्विघात समीकरण

az 2 + bz + c = 0, जहाँ a , b , s वास्तविक संख्याएँ हैं,एक 0, जड़ें हैं। ये जड़ें प्रसिद्ध सूत्र के अनुसार पाई जाती हैं:

जेड 1, 2 =
.

यह भी सत्य है कि घात का कोई भी समीकरणएनबिल्कुल है एन जड़ें, जबकि उनमें से समान और जटिल हो सकती हैं।

गणित के सबसे सुंदर सूत्रों में से एक पर विचार करना असंभव नहीं है - फॉर्म के घन समीकरण की जड़ों की गणना के लिए कार्डानो सूत्रएक्स 3 + पीएक्स + क्यू = 0:

.

उदाहरण 5द्विघात समीकरण को हल करें

विभेदक:

डी<0, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!

दो जड़ें हैं:

संयुग्मी जटिल जड़ें हैं

तो समीकरण दो संयुग्मित जटिल जड़ें हैं: ,

और सामान्य तौर पर, "nth" डिग्री के बहुपद वाले किसी भी समीकरण के बिल्कुल मूल होते हैं, जिनमें से कुछ जटिल हो सकते हैं।

जटिल विमान की अवधारणा।

यदि किसी वास्तविक संख्या को ज्यामितीय रूप से एक संख्या रेखा पर एक बिंदु के रूप में दर्शाया जा सकता है, तो एक जटिल संख्या को समतल पर एक बिंदु द्वारा दर्शाया जाता है, जिसके निर्देशांक क्रमशः जटिल संख्या के वास्तविक और काल्पनिक भाग होंगे।आर वास्तविक संख्याओं के समुच्चय को निरूपित करने की प्रथा है।बहुत साराजटिल आंकड़े आमतौर पर पत्र द्वारा दर्शाया जाता है C. इस स्थिति में, क्षैतिज अक्ष वास्तविक संख्यात्मक अक्ष होगा, और ऊर्ध्वाधर अक्ष काल्पनिक अक्ष होगा।

इस प्रकार, वास्तविक संख्याएँ x-अक्ष पर और o-अक्ष पर स्थित होती हैं Y विशुद्ध रूप से काल्पनिक हैं:

एक ड्राइंग को डिजाइन करने के नियम लगभग एक कार्टेशियन समन्वय प्रणाली में एक ड्राइंग के समान हैं। कुल्हाड़ियों के साथ, आपको आयाम सेट करने की आवश्यकता है, ध्यान दें: शून्य; वास्तविक अक्ष के साथ इकाई; काल्पनिक इकाईकाल्पनिक धुरी के साथ।

उदाहरण 6. सम्मिश्र तल पर निम्नलिखित सम्मिश्र संख्याओं की रचना कीजिए:

वास्तविक संख्याओं का समुच्चयसम्मिश्र संख्याओं के समुच्चय का उपसमुच्चय है।

6. एक जटिल संख्या का ज्यामितीय रूप।

से लैटिन में "जटिल" शब्द का अर्थ है "समग्र", "जटिल"। इस तथ्य के बावजूद कि जटिल संख्याओं के साथ काम करना वास्तविक संख्याओं की तुलना में अधिक कठिन नहीं है, उन्नीसवीं शताब्दी की शुरुआत तक, जटिल संख्याओं को एक बहुत ही जटिल, अस्पष्ट, लगभग रहस्यमय वस्तु के रूप में देखा जाता था। बेहतर उपयोग के योग्य तप के साथ, "काल्पनिक" संख्याओं के समर्थकों और विरोधियों के बीच एक लंबा संघर्ष छेड़ा गया। विरोधियों की मुख्य आपत्ति इस प्रकार थी: रूप की अभिव्यक्तिए+आईबी अर्थहीन क्योंकिमैं एक वास्तविक संख्या नहीं है, और इसलिए एक संख्या बिल्कुल नहीं है; इसीलिएमैं वास्तविक संख्या से गुणा नहीं किया जा सकता है।

जटिल संख्याओं के सिद्धांत को एक ठोस आधार पर रखने के लिए, इसका स्पष्ट निर्माण आवश्यक था, अधिमानतः ज्यामितीय। जटिल संख्याओं के समुच्चय का ज्यामितीय बोध होने की इच्छा आकस्मिक नहीं है, यदि हम याद रखें कि वास्तविक संख्याओं का समुच्चय भी हमारे लिए "वास्तविक रेखा" से एक निश्चित बिंदु के साथ अविभाज्य है जो उस पर 0 का प्रतिनिधित्व करता है, और एक निश्चित के साथ नंबर 1 की स्थिति से निर्धारित पैमाना।

पहली बार, जटिल संख्याओं पर ज्यामितीय संक्रियाओं का निरूपण डेनिश सर्वेक्षक के. वेसल द्वारा 1799 में और स्वतंत्र रूप से 1806 में फ्रांसीसी गणितज्ञ जे. आर्गन द्वारा दिया गया था। हालांकि, जर्मन गणितज्ञ एफ. गॉस और अंग्रेजी गणितज्ञ डब्ल्यू. हैमिल्टन के काम के बाद इसे अठारहवीं शताब्दी के तीसवें दशक में ही सामान्य पहचान मिली। जटिल संख्याओं की ज्यामितीय व्याख्या का विचार यह है कि उन्हें वास्तविक संख्याओं की तरह एक सीधी रेखा के बिंदुओं द्वारा नहीं, बल्कि एक समतल के बिंदुओं द्वारा दर्शाया जाता है।

जटिल संख्याजेड = एक + बी मैं एक समतल पर कार्टेशियन आयताकार निर्देशांक वाले एक बिंदु द्वारा दर्शाया गया है जिसमें निर्देशांक हैं (a;बी)।इस

बिंदु को एक ही अक्षर से दर्शाया जाता हैजेड . वास्तविक संख्याओं को एब्सिस्सा अक्ष के बिंदुओं द्वारा दर्शाया जाता है, और विशुद्ध रूप से काल्पनिक संख्याओं को कोटि अक्ष के बिंदुओं द्वारा दर्शाया जाता है।

एक सम्मिश्र संख्या को उस सम्मिश्र तल पर एक सदिश के रूप में भी दर्शाया जाता है जिसका उद्गम बिंदु पर होता है हेऔर बिंदु M पर समाप्त होता है।

सम्मिश्र संख्याओं के योग का निर्माण सदिश जोड़ के सामान्य नियम के अनुसार किया जाता है, अर्थात समांतर चतुर्भुज नियम के अनुसार

सम्मिश्र संख्याओं का अंतर सदिश घटाव नियम के अनुसार बनाया गया है:

7एक सम्मिश्र संख्या का त्रिकोणमितीय रूप।

मनमाना जटिल संख्याजेड = ए + द्वि त्रिज्या वेक्टर के रूप में दर्शाया गया है
जटिल विमान पर। होने देनाएन - बिंदु प्रक्षेपणएम वास्तविक धुरी के लिए। एक समकोण त्रिभुज में OMN पैर की लंबाई ON और OM क्रमशः बराबरए और बी , और कर्ण की लंबाईओम है
. त्रिकोणमिति से ज्ञात होता है कि पैर की लंबाई और कर्ण की लंबाई का अनुपात शामिल कोण की कोज्या और विपरीत की ज्या के बराबर होता है। फलस्वरूप,

ए = रेज = | जेड | क्योंकि ,

बी = आईएम जेड = | जेड | पाप ,

कहाँ पे φ –
- जटिल संख्या का मुख्य तर्क (चरण, आयाम) जेड , - < φ < (कोनाबीच वास्तविक अक्ष का धनात्मक अर्ध-अक्षरेज और त्रिज्या सदिश मूल बिंदु से संगत बिंदु तक खींचा गया है). तब सम्मिश्र संख्या को निरूपित किया जा सकता हैजैसा:

लेखन के इस रूप को कहा जाता है एक जटिल संख्या का त्रिकोणमितीय रूप।

उदाहरण 7:समाधान:
आइए त्रिकोणमितीय रूप में संख्या का प्रतिनिधित्व करते हैं। इसका मापांक और तर्क खोजें। . चूंकि (केस 1), तब . इस तरह: त्रिकोणमितीय रूप में एक संख्या है।

त्रिकोणमितीय रूप में सम्मिश्र संख्याओं का गुणनफल और भागफल

त्रिकोणमितीय रूप में दी गई सम्मिश्र संख्याओं वाली सभी बीजीय संक्रियाएँ, उसी नियमों के अनुसार निष्पादित किए जाते हैं जैसे बीजगणितीय रूप में दी गई जटिल संख्याओं के साथ। जटिल संख्याओं को जोड़ना और घटाना आसान और अधिक सुविधाजनक होता है जब उन्हें बीजीय रूप में दिया जाता है, और त्रिकोणमितीय रूप में गुणा और विभाजित किया जाता है। तीन प्रमेय हैं।

प्रमेय 1.सम्मिश्र संख्याओं की किसी भी परिमित संख्या को गुणा करते समय, उनके मापांक गुणा किए जाते हैं और तर्क जोड़े जाते हैं।

प्रमेय 2।सम्मिश्र संख्याओं को विभाजित करते समय, उनके मापकों को विभाजित किया जाता है और तर्कों को घटाया जाता है।

प्रमेय 3.चलो z जटिल है, औरएन - प्राकृतिक संख्या। सम्मिश्र संख्याओं के समुच्चय में, व्यंजक
ज़ू में =0 का एकल मान शून्य के बराबर है, और जबजेड 0-एन विभिन्न मूल्य। यदि एकजेड = आर ( क्योंकि +मैं पाप ), तो ये मान सूत्र द्वारा पाए जाते हैं

=
(क्योंकि
+मैं पाप
), \u003d 0.1, ..., एन -1।

उदाहरण 8. एक उत्पाद खोजें: ,

8. सम्मिश्र संख्याओं को घात तक बढ़ाना

एक सम्मिश्र संख्या का वर्ग करना

:

एक सम्मिश्र संख्या के लिए, अपना संक्षिप्त गुणन सूत्र निकालना आसान है:
. अंतर के वर्ग के साथ-साथ योग के घन और अंतर के घन के लिए एक समान सूत्र प्राप्त किया जा सकता है। क्या होगा यदि किसी सम्मिश्र संख्या को 5वीं, 10वीं, या 100वीं घात तक बढ़ाने की आवश्यकता है? यह स्पष्ट है कि बीजगणितीय रूप में ऐसी क्रिया करना व्यावहारिक रूप से असंभव है, वास्तव में, उदाहरण को कैसे हल किया जाए?

और यहाँ एक जटिल संख्या का त्रिकोणमितीय रूप बचाव के लिए आता है और तथाकथित डी मोइवर का सूत्र.

(अब्राहम डी मोइवर (1667 - 1754) - अंग्रेजी गणितज्ञ)।

सम्मिश्र संख्याओं के गुणन की संक्रिया से यह निम्नानुसार है कि

सामान्य तौर पर, हमें मिलता है:

,

कहाँ पे एन – एक सकारात्मक पूर्णांक।

उदाहरण 7. एक सम्मिश्र संख्या दी हुई है, ज्ञात कीजिए।

सबसे पहले आपको दी गई संख्या को त्रिकोणमितीय रूप में प्रस्तुत करना होगा।

फिर, डी मोइवर के सूत्र के अनुसार:

9. एक सम्मिश्र संख्या का घातांकीय रूप

=8 + 6 मैं

10. सम्मिश्र संख्याओं का प्रयोग कहाँ किया जाता है?

पिछले दो सौ वर्षों में, जटिल संख्याओं ने कई, और कभी-कभी पूरी तरह से अप्रत्याशित अनुप्रयोग पाए हैं। इसलिए, उदाहरण के लिए, जटिल संख्याओं की मदद से, गॉस ने एक विशुद्ध रूप से ज्यामितीय प्रश्न का उत्तर पाया: एक कम्पास और एक शासक के साथ एक नियमित n-गॉन का निर्माण किस प्राकृतिक n के लिए किया जा सकता है? स्कूल ज्यामिति पाठ्यक्रम से, यह जाना जाता है कि कम्पास और एक शासक के साथ कुछ नियमित बहुभुज कैसे बनाए जाते हैं: एक नियमित त्रिकोण, एक वर्ग, एक नियमित 6-गॉन (इसकी भुजा इसके चारों ओर घेरे हुए वृत्त की त्रिज्या के बराबर है)। नियमित 5-गॉन और 15-गॉन का निर्माण अधिक कठिन है। कई उल्लेखनीय प्राचीन ग्रीक जियोमीटर और अन्य वैज्ञानिकों के महान प्रयासों के बावजूद, कोई भी नियमित हेप्टागन या नियमित 9-होल बनाने में कामयाब नहीं हुआ। p = 3 और p = 5 को छोड़कर, किसी भी अभाज्य संख्या p के लिए एक नियमित p-gon बनाना भी संभव नहीं था। दो हजार से अधिक वर्षों तक कोई भी इस समस्या को हल करने में आगे नहीं बढ़ सका। 1796 में, गॉटिंगेन विश्वविद्यालय में गणित के एक 19 वर्षीय छात्र कार्ल फ्रेडरिक गॉस ने पहली बार एक कम्पास और स्ट्रेटेज का उपयोग करके एक नियमित 17-गॉन के निर्माण की संभावना को साबित किया। यह गणित के इतिहास की सबसे आश्चर्यजनक खोजों में से एक थी। अगले कुछ वर्षों में, गॉस ने नियमित n-gons के निर्माण की समस्या को पूरी तरह से हल कर दिया। गॉस ने साबित किया कि एक विषम संख्या में पक्षों (कोने) के साथ एक नियमित एन-गॉन का निर्माण कम्पास और स्ट्रेटेज का उपयोग करके किया जा सकता है यदि और केवल अगर एन एक फ़र्मेट प्राइम या कई अलग-अलग फ़र्मेट प्राइम का उत्पाद है। (फर्मेट संख्याएँ F n \u003d + 1 के लिए n \u003d 0, 1, 2, 3, 4 के लिए संख्याएँ हैं, ये संख्याएँ अभाज्य हैं, n \u003d 5 के लिए संख्या F 5 समग्र होगी। इस परिणाम से इसका अनुसरण किया गया कि एन = 7, 9, 11, 13 के लिए एक नियमित बहुभुज का निर्माण असंभव है। यह देखना आसान है कि नियमित एन-गॉन बनाने की समस्या त्रिज्या आर = 1 के एक सर्कल को विभाजित करने की समस्या के बराबर है। n बराबर भागों। एकता से डिग्री।

एक जटिल चर के कार्यों के सिद्धांत का व्यापक रूप से कार्टोग्राफी, इलेक्ट्रिकल इंजीनियरिंग, तापीय चालकता आदि की महत्वपूर्ण व्यावहारिक समस्याओं को हल करने में उपयोग किया जाता है। कई मुद्दों में, जहां हम बात कर रहे हैं, उदाहरण के लिए, आसपास के अंतरिक्ष में बिंदुओं पर विद्युत क्षमता के बारे में आवेशित संधारित्र, या एक गर्म शरीर के अंदर के तापमान के बारे में, एक निश्चित चैनल में प्रवाहित होने वाले तरल या गैस के कणों की गति के बारे में और कुछ बाधाओं के आसपास बहते हुए, आदि, किसी को क्षमता, तापमान, वेगों को खोजने में सक्षम होना चाहिए। आदि। इस तरह की समस्याओं को बिना किसी कठिनाई के हल किया जा सकता है, जब उनके सामने आने वाले निकायों का एक साधारण आकार होता है (उदाहरण के लिए, फ्लैट प्लेट या गोलाकार सिलेंडर के रूप में)।

रूसी और सोवियत वैज्ञानिक एच.ई. ज़ुकोवस्की (1847-1921) ने सफलतापूर्वक आवेदन किया

महत्वपूर्ण लागू समस्याओं के समाधान के लिए एक जटिल चर के कार्यों का सिद्धांत।

इसलिए, इस सिद्धांत के तरीकों का उपयोग करते हुए, उन्होंने एक विमान विंग के लिफ्ट बल के बारे में मुख्य प्रमेय को साबित कर दिया। V. I. लेनिन ने H. E. Zhukovsky को "रूसी विमानन का जनक" कहा। अपने एक भाषण में, एच.ई. ज़ुकोवस्की ने कहा: "... एक व्यक्ति के पास पंख नहीं होते हैं और उसके शरीर के वजन के संबंध में मांसपेशियों के वजन के संबंध में, वह एक पक्षी से 72 गुना कमजोर होता है; ... यह हवा से लगभग 800 गुना भारी है, जबकि एक पक्षी हवा से 200 गुना भारी है। लेकिन, मुझे लगता है कि वह अपनी मांसपेशियों के बल पर नहीं, बल्कि अपने दिमाग के बल पर, उड़ जाएगा। एक जटिल चर के कार्यों के सिद्धांत की सहायता से, एच.ई. ज़ुकोवस्की ने बांधों के माध्यम से पानी के रिसने से संबंधित समस्याओं का समाधान किया।

उच्च गणित के अन्य वर्गों के कार्यों को पूरा करने के लिए जटिल संख्याओं की आवश्यकता होती है, इसके अलावा, व्यवहार में उनका उपयोग काफी भौतिक इंजीनियरिंग गणनाओं में किया जाता है।

11. निष्कर्ष

सामान्य तौर पर, मेरा मानना ​​​​है कि उसके काम का उद्देश्य और कार्य पूरा हो गया है। मैंने खुद इस विषय में महारत हासिल की है। अध्ययन के दौरान, मैंने इस विषय पर बहुत सारे साहित्य का अध्ययन किया। विभिन्न पुस्तकों को पढ़ने के दौरान, मैंने अपने लिए इस विषय पर सबसे दिलचस्प, सरल और सुंदर तथ्यों को नोट किया, साथ ही साथ उन्हें अपने प्रकाश में प्रस्तुत करने की कोशिश की, जिस तरह से मैं सबसे तर्कसंगत मानता हूं।

मेरे काम के लाभों में संक्षिप्तता और प्रस्तुति की सरलता, सम्मिश्र संख्याओं के बारे में ज्ञान का एक साथ एकीकरण, अभिगम्यता शामिल हैं।

मुझे अपना काम उन छात्रों के लिए उपयोगी और प्रासंगिक लगता है जो स्कूली पाठ्यक्रम के बारे में अधिक जानना चाहते हैं।

अध्ययन के दौरान, मैंने अपनी कक्षा में कई सत्र आयोजित किए। लेकिन चूँकि हमारी कक्षा में मेरे अलावा केवल 2 विद्यार्थी हैं, इसलिए ज्ञान की गुणवत्ता में सुधार का पता लगाना संभव नहीं था, क्योंकि वे अच्छा कर रहे हैं। लेकिन मुझे खुशी है कि हर कोई दसवीं कक्षा में इस विषय का अध्ययन जारी रखना चाहता था।

मेरे निष्कर्ष:

1. विभिन्न साहित्यिक स्रोतों का अध्ययन किया गया है, सामग्री का चयन किया गया है जो जटिल संख्याओं का सबसे संपूर्ण चित्र, उनकी खोज का इतिहास, गणित की विभिन्न शाखाओं में उनकी भूमिका और महत्व देता है। इन संख्याओं पर किए गए अंकगणितीय कार्यों को परिभाषित और माना जाता है, उदाहरणों का चयन किया जाता है और जटिल संख्याओं का उपयोग करके हल किया जाता है।

2. कई गणितीय समस्याओं को हल करने में सम्मिश्र संख्याओं के महत्व और भूमिका का अनुमान लगाया जाता है।

3. यदि स्कूल वर्ष की शुरुआत में 9वीं कक्षा के छात्रों के बीच जटिल संख्याओं के बारे में जागरूकता और ज्ञान के स्तर का मूल्यांकन निम्न के रूप में किया जा सकता है, तो स्कूल वर्ष के अंत तक गणित का अध्ययन करने, उनके क्षितिज को व्यापक बनाने, और जटिलता के बढ़े हुए स्तर की कई समस्याओं को सफलतापूर्वक हल करना।

12. सन्दर्भ

1. ए.जी. मोर्दकोविच। बीजगणित और विश्लेषण की शुरुआत। 10 सेल मॉस्को: मेनेमोसिन, 2006।

2. एम। हां। वायगोडस्की; प्राथमिक गणित की हैंडबुक। एम.: स्टेट पब्लिशिंग हाउस ऑफ फिजिकल एंड मैथमैटिकल लिटरेचर, 1960।

3. एन.वाई.ए. विलेनकिन एट अल बीजगणित और गणितीय विश्लेषण। 11 कोशिकाएं मॉस्को: मेनेमोसिन, 2004।

4. ए.जी. मोर्दकोविच। बीजगणित और विश्लेषण की शुरुआत। 10 सेल मॉस्को: मेनेमोसिन, 2006।

5. स्कूल में गणित का इतिहास, जी.आई. ग्लेज़र द्वारा संपादित। - मास्को-1983।

6. गणित के चयनित प्रश्न, IN Antipov द्वारा संपादित। - मास्को-1979।

7. N. Ya. Vilenkin द्वारा संपादित गणित की पाठ्यपुस्तक के पन्नों के पीछे। - मास्को-1996।

8. एन.बी. अल्फुतोव। बीजगणित और संख्या सिद्धांत। एम.: एमटीएसएनएमओ, 2005।

"जटिल संख्या" विषय पर परीक्षण करें

एक सम्मिश्र संख्या में कितने अंकन होते हैं?

ए) 1 बी) 2 सी) 3 डी) 4

एक संख्या क्या हैमैं?

a) एक संख्या जिसका वर्ग 1 . है

b) एक संख्या जिसका वर्ग है - 1

c) एक संख्या जिसका वर्गमूल है - 1

d) एक संख्या जिसका वर्गमूल 1 . है

यदि सम्मिश्र संख्या लिखी जाए तो डी मोइवर का सूत्र लागू किया जा सकता है:

यदि सम्मिश्र संख्या लिखी जाती है तो यूलर सूत्र लागू किया जा सकता है:

ए) एक सांकेतिक रूप में बी) एक दृश्य रूप में

सी) त्रिकोणमितीय रूप डी) बीजगणितीय रूप

एक सम्मिश्र संख्या को संख्या तल पर किस प्रकार निरूपित किया जाता है?

ए) एक खंड के रूप में बी) एक बिंदु या त्रिज्या वेक्टर के रूप में

सी) एक फ्लैट ज्यामितीय आकृति सी) एक सर्कल के रूप में

दिए गए नंबरों में से चुनें पूरी तरह से काल्पनिक:

एक) जेड =3 +6 मैंबी) जेड 2 =6 मैंमें) जेड 2 =31 ग्राम) जेड 2 =0

संख्याओं के योग की गणना करें z 1 =7 +2i और z 2 =3 +7 i

एक ) z =10 +9i b) z =4-5i c) z =10 -5i d) z =4 +5i

8. त्रिकोणमितीय रूप में जटिल संख्या z \u003d 3 + 4i का प्रतिनिधित्व करें

a) त्रिज्या सदिश है b) z =5(0.6 +0.8i )

में) z =3 -4i d) निर्देशांक तल पर एक बिंदु है

9. किस सेट में संख्या 5 शामिल है; 3; -6i;2.7; 2i?

a) वास्तविक संख्या b) परिमेय संख्याएं

c) सम्मिश्र संख्या d) अपरिमेय संख्याएँ

10. "काल्पनिक संख्या" नाम का परिचय किसने दिया?

a) डेसकार्टेस b) आर्गन

सी) यूलर डी) कार्डानो

यदि आपको दो शहरों के बीच की दूरी का नाम देना है, तो आप मील, किलोमीटर, या रैखिक दूरी की अन्य इकाइयों में एक ही संख्या दे सकते हैं। हालांकि, अगर आपको एक शहर से दूसरे शहर तक कैसे जाना है, इसका वर्णन करना होगा, तो आपको मानचित्र पर केवल दो बिंदुओं के बीच की दूरी की तुलना में अधिक जानकारी देने की आवश्यकता है। इस मामले में, यह उस दिशा के बारे में कहने योग्य है जिसमें आपको आगे बढ़ने की आवश्यकता है और इसके बारे में।

एक आयामी आयाम को व्यक्त करने वाली जानकारी को विज्ञान में अदिश राशि कहा जाता है। स्केलर वे संख्याएँ हैं जिनका उपयोग अधिकांश गणितीय गणनाओं में किया जाता है। उदाहरण के लिए, किसी वस्तु का द्रव्यमान और गति अदिश राशियाँ होती हैं।

प्राकृतिक घटनाओं का सफलतापूर्वक विश्लेषण करने के लिए, हमें अमूर्त वस्तुओं और बहुआयामी मात्राओं का प्रतिनिधित्व करने में सक्षम विधियों के साथ काम करना चाहिए। यहां जटिल संख्याओं के पक्ष में अदिश संख्याओं को छोड़ना आवश्यक है। वे एक साथ दो आयामों को व्यक्त करना संभव बनाते हैं।

जटिल संख्याओं को समझना आसान होता है जब उन्हें ग्राफिक रूप से दर्शाया जाता है। यदि किसी रेखा की एक निश्चित लंबाई और दिशा है, तो यह एक चित्रमय निरूपण होगा। इसे आमतौर पर एक वेक्टर के रूप में भी जाना जाता है।

जटिल और अदिश राशियों के बीच अंतर

इस प्रकार की संख्याएँ जैसे पूर्णांक, परिमेय और वास्तविक विद्यालय के बच्चों से परिचित हैं। उन सभी में एक आयामीता है। संख्या रेखा का सीधा होना इसे आलेखीय रूप से दर्शाता है। आप इस पर ऊपर या नीचे जा सकते हैं, लेकिन इस रेखा के साथ सभी "आंदोलन" क्षैतिज अक्ष तक सीमित होंगे। वस्तुओं की संख्या गिनने, वजन व्यक्त करने या बैटरी के डीसी वोल्टेज को मापने के लिए एक-आयामी, अदिश संख्याएं पर्याप्त हैं। लेकिन उनका मतलब कुछ और जटिल नहीं हो सकता। स्केलर एक साथ दो शहरों के बीच की दूरी और दिशा या चरण के साथ आयाम को व्यक्त नहीं कर सकते। इस प्रकार की संख्याओं को पहले से ही मानों की बहुआयामी श्रेणी के रूप में निरूपित करना आवश्यक है। दूसरे शब्दों में, हमें सदिश राशियों की आवश्यकता होती है जिनमें न केवल परिमाण हो सकता है, बल्कि प्रसार की दिशा भी हो सकती है।

निष्कर्ष

एक अदिश संख्या एक प्रकार की गणितीय वस्तु है जिसे लोग रोजमर्रा की जिंदगी में उपयोग करने के आदी हैं - यह तापमान, लंबाई, वजन आदि है। सम्मिश्र संख्या एक ऐसा मान है जिसमें दो प्रकार के डेटा शामिल होते हैं।

एक वेक्टर एक जटिल संख्या का ग्राफिक प्रतिनिधित्व है। यह एक प्रारंभिक बिंदु और एक परिभाषित लंबाई और दिशा के साथ एक तीर जैसा दिखता है। कभी-कभी "वेक्टर" शब्द का प्रयोग रेडियो इंजीनियरिंग में किया जाता है, जहां यह संकेतों के बीच चरण बदलाव को व्यक्त करता है।

सम्मिश्र संख्याओं के बारे में आवश्यक जानकारी को याद करें।

जटिल संख्यारूप की अभिव्यक्ति है एक + द्वि, कहाँ पे एक, बीवास्तविक संख्याएं हैं, और मैं- तथाकथित काल्पनिक इकाई, वह प्रतीक जिसका वर्ग -1 है, अर्थात। मैं 2 = -1। संख्या एकबुलाया असली हिस्सा, और संख्या बी - काल्पनिक हिस्साजटिल संख्या जेड = एक + द्वि. यदि एक बी= 0, फिर . के बजाय एक + 0मैंसरलता से लिखो एक. यह देखा जा सकता है कि वास्तविक संख्याएँ सम्मिश्र संख्याओं की एक विशेष स्थिति होती हैं।

सम्मिश्र संख्याओं पर अंकगणितीय संक्रियाएँ वास्तविक संख्याओं की तरह ही होती हैं: उन्हें एक दूसरे से जोड़ा, घटाया, गुणा और विभाजित किया जा सकता है। जोड़ और घटाव नियम के अनुसार आगे बढ़ते हैं ( एक + द्वि) ± ( सी + डि) = (एक ± सी) + (बी ± डी)मैं, और गुणा - नियम के अनुसार ( एक + द्वि) · ( सी + डि) = (एसी – बीडीओ) + (विज्ञापन + बीसी)मैं(यहाँ बस यही प्रयोग किया गया है कि मैं 2 = -1)। संख्या = एक – द्विबुलाया जटिल सन्युग्मप्रति जेड = एक + द्वि. समानता जेड · = एक 2 + बी 2 आपको यह समझने की अनुमति देता है कि एक सम्मिश्र संख्या को दूसरी (गैर-शून्य) सम्मिश्र संख्या से कैसे विभाजित किया जाए:

(उदाहरण के लिए, .)

जटिल संख्याओं का एक सुविधाजनक और दृश्य ज्यामितीय प्रतिनिधित्व होता है: संख्या जेड = एक + द्विनिर्देशांक के साथ एक वेक्टर के रूप में प्रतिनिधित्व किया जा सकता है ( एक; बी) कार्तीय तल पर (या, जो लगभग समान है, एक बिंदु - इन निर्देशांकों के साथ सदिश का अंत)। इस स्थिति में, दो सम्मिश्र संख्याओं के योग को संबंधित सदिशों के योग के रूप में दर्शाया जाता है (जिसे समांतर चतुर्भुज नियम द्वारा पाया जा सकता है)। पाइथागोरस प्रमेय द्वारा, निर्देशांक के साथ वेक्टर की लंबाई ( एक; बी) के बराबर है । इस मान को कहा जाता है मापांकजटिल संख्या जेड = एक + द्विऔर द्वारा निरूपित किया जाता है | जेड|. यह सदिश x-अक्ष की धनात्मक दिशा के साथ जो कोण बनाता है (वामावर्त गिना जाता है) कहलाता है बहसजटिल संख्या जेडऔर Arg . द्वारा निरूपित जेड. तर्क को विशिष्ट रूप से परिभाषित नहीं किया गया है, लेकिन केवल 2 . के गुणज के योग तक ही π रेडियन (या 360°, यदि आप डिग्री में गिनते हैं) - आखिरकार, यह स्पष्ट है कि मूल के चारों ओर इस तरह के कोण से घूमने से वेक्टर नहीं बदलेगा। लेकिन अगर लंबाई का सदिश आरएक कोण बनाता है φ x-अक्ष की धनात्मक दिशा के साथ, तो इसके निर्देशांक बराबर होते हैं ( आरक्योंकि φ ; आरपाप φ ) इसलिए यह पता चला है त्रिकोणमितीय संकेतनजटिल संख्या: जेड = |जेड| (क्योंकि(अर्ग .) जेड) + मैंपाप(अर्ग जेड))। इस रूप में जटिल संख्याएँ लिखना अक्सर सुविधाजनक होता है, क्योंकि यह गणनाओं को बहुत सरल करता है। त्रिकोणमितीय रूप में सम्मिश्र संख्याओं का गुणन बहुत सरल लगता है: जेडएक · जेड 2 = |जेड 1 | · | जेड 2 | (क्योंकि(अर्ग .) जेड 1+आर्ग जेड 2) + मैंपाप(अर्ग जेड 1+आर्ग जेड 2)) (दो सम्मिश्र संख्याओं को गुणा करते समय, उनके मापांक गुणा किए जाते हैं और तर्क जोड़े जाते हैं)। यहां से फॉलो करें डी मोइवर सूत्र: जेड एन = |जेड|एन(क्योंकि( एन(आर्गो जेड)) + मैंपाप ( एन(आर्गो जेड)))। इन सूत्रों की सहायता से सम्मिश्र संख्याओं से किसी भी अंश के मूल निकालना सीखना आसान है। z . का nवां मूलइतनी जटिल संख्या है वू, क्या डब्ल्यू नहीं = जेड. यह स्पष्ट है कि , और कहाँ कसेट से कोई भी मान ले सकते हैं (0, 1, ..., एन- एक)। इसका मतलब है कि हमेशा सटीक होता है एनजड़ों एनएक सम्मिश्र संख्या से वें डिग्री (विमान पर वे एक नियमित के शीर्ष पर स्थित होते हैं एन-गॉन)।

पिछले दो सौ वर्षों में, जटिल संख्याओं ने कई, और कभी-कभी पूरी तरह से अप्रत्याशित अनुप्रयोग पाए हैं। इसलिए, उदाहरण के लिए, जटिल संख्याओं की मदद से, गॉस ने एक विशुद्ध रूप से ज्यामितीय प्रश्न का उत्तर पाया: एक कम्पास और एक शासक के साथ एक नियमित n-गॉन का निर्माण किस प्राकृतिक n के लिए किया जा सकता है? स्कूल ज्यामिति पाठ्यक्रम से, यह ज्ञात है कि एक कम्पास और एक शासक के साथ कुछ नियमित बहुभुज कैसे बनाए जाते हैं: एक नियमित त्रिकोण, एक वर्ग, एक नियमित षट्भुज (इसकी भुजा इसके चारों ओर घेरे हुए वृत्त की त्रिज्या के बराबर है)। अधिक कठिन एक नियमित पेंटागन और पंद्रह-गॉन का निर्माण है। इन नियमित बहुभुजों को बनाने का तरीका सीखने के बाद, संबंधित बहुभुजों के निर्माण के लिए आगे बढ़ना आसान है जिसमें पक्षों की संख्या दोगुनी है: एक अष्टकोण, एक दशहरा, आदि। इन सभी निर्माण समस्याओं को प्राचीन ग्रीस में हल किया गया था। हालांकि, कई उल्लेखनीय प्राचीन ग्रीक जियोमीटर और अन्य वैज्ञानिकों के महान प्रयासों के बावजूद, कोई भी नियमित हेप्टागन या नियमित नॉनगोन बनाने में कामयाब नहीं हुआ। पी = 3 और पी = 5 को छोड़कर, किसी भी अभाज्य संख्या पी के लिए एक नियमित पी-गॉन का निर्माण करना भी संभव नहीं था। दो हजार से अधिक वर्षों तक, कोई भी इस समस्या को हल करने में आगे नहीं बढ़ सका। 1796 में, गॉटिंगेन विश्वविद्यालय में 19 वर्षीय गणित के छात्र कार्ल फ्रेडरिक गॉस ने पहली बार एक कम्पास और सीधा का उपयोग करके एक नियमित सत्रह-पक्षीय त्रिभुज के निर्माण की संभावना को साबित किया। यह गणित के इतिहास की सबसे आश्चर्यजनक खोजों में से एक थी। अगले कुछ वर्षों में, गॉस ने नियमित n-gons के निर्माण की समस्या को पूरी तरह से हल कर दिया।

गॉस ने साबित किया कि एक विषम संख्या में पक्षों (कोने) के साथ एक नियमित एन-गॉन का निर्माण एक कंपास और स्ट्रेटेज का उपयोग करके किया जा सकता है यदि और केवल अगर एन एक फ़र्मेट प्राइम या कई अलग-अलग फ़र्मेट प्राइम का उत्पाद है। (फर्मैट संख्याएं एफ एन = + 1 के रूप की संख्याएं हैं एन = 0, 1, 2, 3, 4 के लिए ये संख्याएं प्रमुख हैं, एन = 5 के लिए संख्या एफ 5 मिश्रित होगी। इस परिणाम से यह निर्माण हुआ कि निर्माण N = 7, 9, 11, 13 के लिए एक नियमित बहुभुज असंभव है।

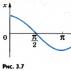
यह देखना आसान है कि एक नियमित n-gon के निर्माण की समस्या त्रिज्या R = 1 के एक वृत्त को n बराबर भागों में विभाजित करने की समस्या के बराबर है। यह ऊपर दिखाया गया था कि एकता के nवें मूल में ठीक n मान होते हैं; इनमें से लगभग सभी मान (एक या दो को छोड़कर) जटिल हैं। एकता से nवीं डिग्री की जड़ों का प्रतिनिधित्व करने वाले बिंदु त्रिज्या R = 1 के एक वृत्त पर स्थित होते हैं और इसे n बराबर चापों में विभाजित करते हैं, अर्थात, वे इस वृत्त में अंकित एक नियमित n-gon के शीर्ष होते हैं (चित्र 3 देखें)। ) एक नियमित 17-गॉन के निर्माण की संभावना को साबित करते हुए, गॉस ने एकता की 17 वीं जड़ों के गुणों का उपयोग किया।

XVIII सदी में। गणित का एक नया क्षेत्र उत्पन्न हुआ - एक जटिल चर के कार्यों का सिद्धांत। आइए हम ऐसे फ़ंक्शन की अवधारणा का परिचय दें। दो जटिल चरों पर विचार करें z = x + मैंवाई और डब्ल्यू = यू + मैं v, जहाँ x, y, u, v वास्तविक चर हैं, मैं= - काल्पनिक इकाई। हम दो जटिल विमानों ऑक्सी (प्लेन जेड), ओ "यूवी (प्लेन डब्ल्यू) को उन पर चुने गए आयताकार समन्वय प्रणालियों के साथ तय करते हैं और इन विमानों पर दो सेट: डी और डी" क्रमशः (चित्र 4)।

डी "

डी

यदि, कुछ नियम f के अनुसार, प्रत्येक बिंदु zD एक बिंदु wD से जुड़ा है", तो हम कहते हैं कि w, z का एक फलन है और लिखते हैं: w = f(z)। इस मामले में सेट D को कहा जाता है समारोह का दायरा w = f(z) जिसका मान डोमेन D से संबंधित है। यदि मानों का सेट f(z) पूरे सेट D को समाप्त कर देता है, तो D” कहलाता है मूल्यों का सेट(परिवर्तन की सीमा) फलन f(z) का। इस मामले में, वे लिखते हैं: डी "= एफ (डी)। सेट डी और डी" को एक ही जटिल विमान पर चित्रित किया जा सकता है। प्रत्येक सेट डी और डी" पूरे विमान के साथ मेल खा सकता है।

इस प्रकार, प्रत्येक जटिल कार्य एक सेट के दूसरे पर एकतरफा मानचित्रण लागू करता है। इसके कारण, जटिल कार्यों को हाइड्रोडायनामिक्स और वायुगतिकी जैसे विज्ञानों में महत्वपूर्ण अनुप्रयोग मिलते हैं, क्योंकि वे तरल (या गैस) की मात्रा के आंदोलन का वर्णन करने के लिए सुविधाजनक होते हैं।

एक जटिल चर के कार्यों के सिद्धांत का उपयोग करते हुए, हम निम्नलिखित महत्वपूर्ण प्रमेय को सिद्ध करते हैं, जिसे लंबे समय तक बीजगणित का मौलिक प्रमेय कहा जाता था।

प्रमेय: किसी भी संख्यात्मक गुणांक वाले किसी भी बहुपद, जिसकी डिग्री एक से कम नहीं है, सामान्य केस कॉम्प्लेक्स में कम से कम एक रूट होता है।

डिग्री n (n ≥ 1) के बहुपद पर विचार करें:

f(x) = a 0 x n + a 1 x n -1 + ... + a n -1 x + a n। (36)

बहुपद की जड़ऐसे नंबर पर कॉल करें c (सामान्य स्थिति में, जटिल: c \u003d a + b मैं), जो दिए गए बहुपद को गायब कर देता है:

ए 0 सी एन + ए 1 सी एन -1 + … + ए एन -1 सी + ए एन ≡ 0।

दूसरे शब्दों में, प्रमेय कहता है कि nवीं डिग्री का एक बीजीय समीकरण (n 1)

ए 0 एक्स एन + ए 1 एक्स एन -1 + ... + ए एन -1 एक्स + ए एन = 0 37)

कम से कम एक जड़ है।

इसका तात्पर्य यह है कि nवीं डिग्री के किसी भी बीजीय समीकरण के ठीक n मूल होते हैं। दरअसल, यदि बहुपद f (x) \u003d a 0 x n + a 1 x n -1 + ... + a n -1 x + a n, का मूल α 1 है, तो इसे f (x) \u003d के रूप में दर्शाया जा सकता है (x - α 1) φ 1 (x), जहां 1 (x) डिग्री n-1 का बहुपद है। इस प्रमेय के अनुसार, इस बहुपद का कम से कम एक मूल है। बहुपद φ 1 (x) से α 2 तक के मूल को निरूपित करें, फिर φ 1 (x) = (x - α 2)φ 2 (x), जहां 2 (x) डिग्री n - 2 का बहुपद है। इसी तरह के तर्क से हम पाते हैं कि f(x) = a 0 (x – a 1)(x – a 2)...(x – a n)। इससे पता चलता है कि f(α i) = 0 के लिए i - 1, 2, ..., n, यानी α i बहुपद (36) या समीकरण (37) के मूल हैं। इस प्रकार, समीकरण (37) के n मूल हैं।

ध्यान दें कि वास्तविक गुणांक वाले किसी भी बहुपद के सम्मिश्र मूल सदैव संयुग्मी होते हैं: यदि c = a - b मैंसमीकरण का मूल है, तो c \u003d a-b मैंइस समीकरण की जड़ भी है। दूसरे शब्दों में, इस तरह के बहुपद की जटिल जड़ें इसकी जड़ों के सेट में जोड़े में होती हैं। इसका तात्पर्य यह है कि विषम कोटि के किसी भी बीजीय समीकरण का कम से कम एक वास्तविक मूल होता है।

टिप्पणी . हर समीकरण की जड़ें वास्तविक या जटिल नहीं होती हैं। उदाहरण के लिए, अनुवांशिक (गैर-बीजगणितीय) समीकरण a x \u003d 0 (a\u003e 0) की कोई जड़ें नहीं हैं (न तो वास्तविक और न ही जटिल)।

किसी सम्मिश्र चर के फलन का सरलतम उदाहरण रैखिक फलन w = z + c है, जहाँ c एक स्थिरांक (जटिल संख्या) है। यह फ़ंक्शन z प्लेन को w प्लेन में बदल देता है। प्रत्येक बिंदु z से वह बिंदु w = z + c को जोड़ती है। जाहिर है, कोई व्यक्ति वेक्टर द्वारा स्थानांतरित (समानांतर अनुवाद) द्वारा बिंदु z से बिंदु w तक जा सकता है साथ, अर्थात बिंदु z को सदिश की दिशा में ले जाकर साथइस वेक्टर की लंबाई के बराबर दूरी पर (चित्र 5)। कोई भी पारी संख्या c के उपयुक्त विकल्प द्वारा प्राप्त की जा सकती है। उदाहरण के लिए, यदि बिंदु z को दो इकाइयों द्वारा ऑक्स अक्ष की सकारात्मक दिशा में स्थानांतरित करने की आवश्यकता है, तो c = 2 लिया जाना चाहिए; बिंदु w = z + 2 वांछित होगा (चित्र 6)। यदि बिंदु z को ओए अक्ष की ऋणात्मक दिशा में तीन इकाई स्थानांतरित करने की आवश्यकता है, तो हम c = -3 लेते हैं मैं; बिंदु w "= z + (-3 .) मैं) = जेड - 3 मैंवांछित होगा (चित्र 6)। तो, फलन w = z + c समतल का रूपांतरण (मानचित्रण) करता है, जिसे सदिश द्वारा शिफ्ट कहा जाता है। साथ.

डब्ल्यू = जेड + सी

डब्ल्यू = जेड + 2

डब्ल्यू" = जेड - 3मैं

एक ज्यामितीय परिवर्तन जिसमें रूपांतरित आकृति में निहित किन्हीं दो रेखाओं के बीच के कोण नहीं बदलते हैं, कहलाते हैं अनुरूप परिवर्तनया अनुरूप मानचित्रण. (किसी बिंदु पर प्रतिच्छेद करने वाली दो रेखाओं के बीच के कोण को उस बिंदु पर खींची गई इन रेखाओं की स्पर्शरेखाओं के बीच के कोण के रूप में समझा जाता है।) अनुरूप मानचित्रण के उदाहरण अनुवाद (समानांतर अनुवाद), समरूपता और रोटेशन हैं। इस प्रकार, हम कह सकते हैं कि फ़ंक्शन w = z + c एक अनुरूप मानचित्रण करता है; यह उन विशेषताओं में से एक है।

एक जटिल चर के कार्यों के सिद्धांत का व्यापक रूप से कार्टोग्राफी, इलेक्ट्रिकल इंजीनियरिंग, तापीय चालकता आदि की महत्वपूर्ण व्यावहारिक समस्याओं को हल करने में उपयोग किया जाता है। कई मुद्दों में, जहां हम बात कर रहे हैं, उदाहरण के लिए, आसपास के अंतरिक्ष में बिंदुओं पर विद्युत क्षमता के बारे में आवेशित संधारित्र, या एक गर्म शरीर के अंदर के तापमान के बारे में, एक निश्चित चैनल में प्रवाहित होने वाले तरल या गैस के कणों की गति के बारे में और कुछ बाधाओं के आसपास बहते हुए, आदि, किसी को क्षमता, तापमान, वेगों को खोजने में सक्षम होना चाहिए। आदि। इस तरह की समस्याओं को बिना किसी कठिनाई के हल किया जा सकता है, जब उनके सामने आने वाले निकायों का एक साधारण आकार होता है (उदाहरण के लिए, फ्लैट प्लेट या गोलाकार सिलेंडर के रूप में)। हालांकि, कई अन्य मामलों में गणना करने में सक्षम होना आवश्यक है। उदाहरण के लिए, एक हवाई जहाज को डिजाइन करने के लिए, किसी को हवाई जहाज के पंख के चारों ओर प्रवाह में कणों के वेगों की गणना करने में सक्षम होना चाहिए। बेशक, विमान की उड़ान के दौरान, हवा के कण और पंख दोनों ही चलते हैं। हालांकि, यांत्रिकी के नियमों पर भरोसा करते हुए, अध्ययन को उस मामले में कम किया जा सकता है जब पंख गतिहीन होता है, और एक वायु प्रवाह उस पर चलता है और उसके चारों ओर बहता है। क्रॉस सेक्शन (विंग प्रोफाइल) में एक एयरक्राफ्ट विंग का फॉर्म चित्र 7 में दिखाया गया है। वेगों की गणना काफी सरल है जब सुव्यवस्थित शरीर का क्रॉस सेक्शन एक वृत्त होता है (अर्थात शरीर स्वयं एक गोल सिलेंडर होता है)। एक विमान के पंख के चारों ओर बहने वाली वायु धारा के कण वेग की समस्या को एक गोल सिलेंडर के चारों ओर प्रवाह की एक सरल समस्या को कम करने के लिए, चित्रा 7 में छायांकित विमान के हिस्से को अनुरूप रूप से मैप करने के लिए पर्याप्त है, (विंग के बाहर) ) चित्र 7, b (वृत्त के बाहर) में छायांकित एक अन्य आकृति पर। इस तरह की मैपिंग एक जटिल चर के कुछ फ़ंक्शन का उपयोग करके की जाती है। इस फ़ंक्शन का ज्ञान एक वृत्ताकार सिलेंडर के चारों ओर प्रवाह में वेग से एक विमान के पंख के पिछले प्रवाह में वेग से गुजरना संभव बनाता है, और इस तरह समस्या को पूरी तरह से हल करता है।

एक जटिल चर के संबंधित कार्य द्वारा दिया गया अनुरूप मानचित्रण, इसी तरह किसी को मनमाना आकार (किसी भी अनुभाग प्रोफ़ाइल) के निकायों के मामले से विद्युत क्षमता और तापमान की गणना करने की समस्याओं के समाधान को कम करने की अनुमति देता है, जिसके लिए सबसे सरल मामलों में समस्याओं का आसानी से समाधान हो जाता है।

रूसी और सोवियत वैज्ञानिक एच.ई. ज़ुकोवस्की (1847-1921) ने महत्वपूर्ण व्यावहारिक समस्याओं के समाधान के लिए एक जटिल चर के कार्यों के सिद्धांत को सफलतापूर्वक लागू किया। इसलिए, इस सिद्धांत के तरीकों का उपयोग करते हुए, उन्होंने एक विमान विंग के लिफ्ट बल के बारे में मुख्य प्रमेय को साबित कर दिया। V. I. लेनिन ने H. E. Zhukovsky को "रूसी विमानन का जनक" कहा। अपने एक भाषण में, एच.ई. ज़ुकोवस्की ने कहा: "... एक व्यक्ति के पास पंख नहीं होते हैं और उसके शरीर के वजन के संबंध में मांसपेशियों के वजन के संबंध में, वह एक पक्षी से 72 गुना कमजोर होता है; ... यह हवा से लगभग 800 गुना भारी है, जबकि एक पक्षी हवा से 200 गुना भारी है। लेकिन, मुझे लगता है कि वह अपनी मांसपेशियों के बल पर नहीं, बल्कि अपने दिमाग के बल पर, उड़ जाएगा। (ज़ुकोवस्की एन.ई. कलेक्टेड वर्क्स। - एम। - एल।: गोस्टेखिज़दत, 1950। -टी। 7. - पी। 16.) एक जटिल चर एच.ई. के कार्यों के सिद्धांत का उपयोग करना। ज़ुकोवस्की ने बांधों के माध्यम से पानी के रिसने से संबंधित समस्याओं का समाधान किया।

विजयी साहित्य की सूची:

"बीजगणित" एस। लेंग पब्लिशिंग हाउस एमआईआर, मॉस्को, 1968

"रिंग्स एंड मॉड्यूल्स" लैंबेक, जोचैम। पब्लिशिंग हाउस एमआईआर, मॉस्को, 1971

"रिंग्स (थ्योरी के तत्व)", मिखलेविच श्री ख। डौगवपिल्स पेडागोगिकल इंस्टीट्यूट पब्लिशिंग हाउस, 1973

"बीजगणित: छल्ले, मॉड्यूल और श्रेणियां" फीस के।, एमआईआर पब्लिशिंग हाउस, 1977

"अंगूठियां और मॉड्यूल। संभाव्यता सिद्धांत की सीमा प्रमेय ”लेनिनग्राद स्टेट यूनिवर्सिटी का प्रकाशन गृह, 1986

"द थ्योरी ऑफ रिंग्स", एन. जैकबसन। स्टेट पब्लिशिंग हाउस ऑफ फॉरेन लिटरेचर, मॉस्को, 1947।