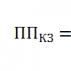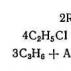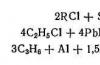Существуют различные методики для построения квадратов порядка одинарной четности и двойной четности.
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 6x6 n=6, а его магическая константа:
- Магическая константа = / 2
- Магическая константа = / 2
- Магическая константа = (6 * 37) / 2
- Магическая константа = 222/2
- Магическая константа квадрата 6х6 равна 111.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Разделите магический квадрат на четыре квадранта одинакового размера. Обозначьте квадранты через А (сверху слева), C (сверху справа), D (снизу слева) и B (снизу справа). Чтобы выяснить размер каждого квадранта, разделите n на 2.
- Таким образом, в квадрате 6х6 размер каждого квадранта равен 3x3.
В квадранте А напишите четвертую часть всех чисел; в квадранте В напишите следующую четвертую часть всех чисел; в квадранте С напишите следующую четвертую часть всех чисел; в квадранте D напишите заключительную четвертую часть всех чисел.
- В нашем примере квадрата 6х6 в квадранте А напишите числа 1-9; в квадранте В - числа 10-18; в квадранте С - числа 19-27; в квадранте D - числа 28-36.
Числа в каждом квадранте записывайте так, как вы строили нечетный квадрат. В нашем примере квадрант А начните заполнять числами с 1, а квадранты С, B, D - с 10, 19, 28, соответственно.
- Число, с которого вы начинаете заполнение каждого квадранта, всегда пишите в центральной ячейке верхней строки определенного квадранта.
- Заполняйте каждый квадрант числами так, как будто это отдельный магический квадрат. Если при заполнении квадранта доступна пустая ячейка из другого квадранта, игнорируйте этот факт и пользуйтесь исключениями из правила заполнения нечетных квадратов.
Выделите определенные числа в квадрантах А и D. На данном этапе сумма чисел в столбцах, строках и по диагонали не будет равна магической константе. Поэтому вы должны поменять местами числа в определенных ячейках верхнего левого и нижнего левого квадрантов.
- Начиная с первой ячейки верхней строки квадранта А, выделите количество ячеек, равное медиане количества ячеек во всей строке. Таким образом, в квадрате 6x6 выделите только первую ячейку верхней строки квадранта А (в этой ячейке написано число 8); в квадрате 10х10 вам нужно выделить первые две ячейки верхней строки квадранта А (в этих ячейках написаны числа 17 и 24).
- Образуйте промежуточный квадрат из выделенных ячеек. Так как в квадрате 6х6 вы выделили только одну ячейку, то промежуточный квадрат будет состоять из одной ячейки. Назовем этот промежуточный квадрат как A-1.
- В квадрате 10х10 вы выделили две ячейки верхней строки, поэтому необходимо выделить две первые ячейки второй строки, чтобы образовать промежуточный квадрат 2х2, состоящий из четырех ячеек.
- В следующей строке пропустите число в первой ячейке, а затем выделите столько чисел, сколько вы выделили в промежуточном квадрате A-1. Полученный промежуточный квадрат назовем A-2.
- Получение промежуточного квадрата А-3 аналогично получению промежуточного квадрата A-1.
- Промежуточные квадраты А-1, А-2, А-3 образуют выделенную область А.
- Повторите описанный процесс в квадранте D: создайте промежуточные квадраты, которые образуют выделенную область D.
МАГИЧЕСКИЕ КВАДРАТЫ
Родиной магических квадратов считают Китай. В Китае существует учение Фэн-шуй, согласно которому цвет, форма и физическое расположение каждого элемента в пространстве влияет на поток Ци, замедляя его, перенаправляя его или ускоряя его, что напрямую влияет на уровень энергии жителей. Для познания тайн мира боги послали императору Ю (Yu) древнейший символ, квадрат Ло Шу (Ло – река).
МАГИЧЕСКИЙ КВАДРАТ ЛО ШУ

Легенда гласит, что около четырех тысяч лет назад из бурных вод реки Ло вышла большая черепаха Шу. Люди, приносящие жертвы реке, увидели черепаху и сразу признали ее божеством. Соображения древних мудрецов показались императору Ю настолько резонными, что он приказал увековечить изображение черепахи на бумаге и скрепил его своей императорской печатью. А иначе как бы мы об этом событии узнали?
Эта черепаха на самом деле была особенной, потому что на ее панцире был нанесен странный узор из точек. Точки были нанесены упорядоченно, это привело древних философов к мысли о том, что квадрат с числами на панцире черепахи служит моделью пространства – картой мира, составленной мифическим основателем китайской цивилизации Хуан-ди. В самом деле, сумма чисел по столбцам, строкам, обеим диагоналям квадрата одинакова M=15 и равна числу дней в каждом из 24-х циклов китайского солнечного года.
Четные и нечетные номера чередуются: причем 4 четных числа (пишутся снизу вверх по убыванию) находятся в четырех углах, а 5 нечетных чисел (пишутся снизу вверх по возрастанию) образуют крест в центре площади. Пять элементов креста отражают землю, огонь, металл, воду и лес. Сумма любых разделенных центром двух чисел равна числу Хо Ти, т.е. десяти.
Четные числа (символы Земли) Ло Шу были нанесены на теле черепахи в виде черных точек, или Инь символов, а нечетные числа (символы Неба) – в виде белых точек, или Ян символов. Земля 1 (или вода) находится снизу, огонь 9 (или небо) – сверху. Не исключено, что современное изображение цифры 5, размещенной в центре композиции, обязано китайскому символу двуединственности Ян и Инь.

МАГИЧЕСКИЙ КВАДРАТ ИЗ КХАДЖУРАХО

Восточная комната
Магия Джозефа Редьярда Киплинга, создавшего образы Маугли, Багиры, Балу, Шер-Хана и, конечно, Табаки, началась накануне двадцатого века. За полстолетия до этого, в феврале 1838, года молодой британский офицер бенгальских инженерных войск Т.С. Берт, заинтересованный разговором слуг, несших его паланкин, отклонился от маршрута и наткнулся на древние храмы в джунглях Индии.
На ступенях храма Вишванатха офицер нашел надпись, свидетельствующую о древности сооружений. Спустя короткое время энергичный генерал-майор А. Каннингем начертил подробные планы Кхаджурахо. Были начаты раскопки, увенчавшиеся сенсационным открытием 22 храмов. Возвели храмы махараджи их династии Чанделов. После распада их царства джунгли поглотили постройки на тысячу лет. Найденный среди изображений обнаженных богов и богинь квадрат четвертого порядка поражал воображение.
Мало того, что у этого квадрата суммы по строкам, столбцам и диагоналям совпадали и равнялись 34. Они совпадали также по ломанным диагоналям, образующимся при сворачивании квадрата в тор, причем в обоих направлениях. За подобное колдовство цифр такие квадраты называют «дьявольскими» (или «пандиагональными», или «насик»).
Безусловно, это свидетельствовало о необычных математических способностях их создателей, превосходящих колонизаторов. Что неизбежно почувствовали люди в белых пробковых шлемах.
МАГИЧЕСКИЙ КВАДРАТ ДЮРЕРА
Знаменитый немецкий художник начала XVI века Альбрехт Дюрер составил первый в европейском искусстве магический квадрат 4х4. Сумма чисел в любой строке, столбце, диагонали, а также, что удивительно, в каждой четверти (даже в центральном квадрате) и даже сумма угловых чисел равна 34. Два средних числа в нижнем ряду указывают дату создания картины (1514). В средних квадратах первого столбика внесены исправления – цифры деформированы.
В картине с оккультной крылатой мышью Сатурном магический квадрат сложен крылатым разумом Юпитером, которые друг другу противостоят. Квадрат симметричен, так как сумма любых двух входящих в него чисел, расположенных симметрично относительно его центра, равна 17. Если сложить четыре числа, полученные ходом шахматного коня – будет 34. Воистину этот квадрат своей безупречной упорядоченностью отражает меланхолию, охватившую художника.

Утренний сон.
Европейцев с удивительными числовыми квадратами познакомил византийский писатель и языковед Мосхопулос. Его работа была специальным сочинением на эту тему и содержала примеры магических квадратов автора.
СИСТЕМАТИЗАЦИЯ МАГИЧЕСКИХ КВАДРАТОВ
В середине XVI в. в Европе появились сочинения, в которых в качестве объектов математического исследования предстали магические квадраты. Затем последовало множество других работ, в частности таких известных математиков, основоположников современной науки, как Штифель, Баше, Паскаль, Ферма, Бесси, Эйлер, Гаусс.
Магический , или волшебный квадрат – это квадратная таблица, заполненная n 2 числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Определение условное, поскольку древние придавали также значение, например, цвету.
Нормальным называется магический квадрат, заполненный целыми числами от 1 до n 2 . Нормальные магические квадраты существуют для всех порядков, за исключением n = 2 , хотя случай n = 1 тривиален – квадрат состоит из одного числа.
Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
M = n (n 2 + 1) /2
Первые значения магических констант приведены в таблице
Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим . Магический квадрат называется ассоциативным или симметричным , если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n 2 + 1 .
Существует только один нормальный квадрат третьего порядка. Его знали многие народы. Расположение чисел в квадрате Ло Шу сходно с символическими обозначениями духов в каббале и знаками индейской астрологии.
Известен также как квадрат Сатурна. Некоторые тайные общества в Средние века видели в нем "каббалу девяти палат". Несомненно, оттенок запретного волшебства много значил для сбережения его изображений.
Он был важен в средневековой нумерологии, часто использовался как амулет или средство для гадания. Каждая ячейка его отвечает мистической букве или иному символу. Прочитанные вместе вдоль определенной линии, эти знаки передавали оккультные сообщения. Цифры, составляющие дату рождения, расставлялись в ячейках квадрата и затем расшифровывались в зависимости от значения и местоположения цифр.
Среди пандиагональных, как их именуют еще, дьявольских магических квадратов выделяют симметричные – идеальные. Дьявольский квадрат остается дьявольским, если производить его поворот, отражение, перестановку строки сверху вниз и наоборот, зачеркивание столбца справа или слева с приписыванием его с противоположной стороне. Всего выделяют пять преобразований, схема последнего приведена на рисунке
Существует 48 дьявольских квадратов 4×4 с точностью до поворотов и отражений. Если принять во внимание еще и симметрию относительно торических параллельных переносов, то остается только три существенно различных дьявольских квадрата 4×4:
Клод Ф. Брэгдон, известный американский архитектор, обнаружил, что, соединив одну за другой клетки только с четными или только с нечетными числами магических квадратов ломаной, мы в большинстве случаев получим изящный узор. Придуманный им узор для вентиляционной решетки в потолке Торговой палаты в Рочестере (штат Нью-Йорк), где он жил, построен из магической ломаной талисмана Ло-Шу. Брэгдон использовал «магические линии» как образцы рисунков для тканей, книжных обложек, архитектурных украшений и декоративных заставок.
Если из одинаковых дьявольских квадратов выложить мозаику (каждый квадрат должен вплотную примыкать к своим соседям), то получится нечто вроде паркета, в котором числа, стоящие в любой группе клеток 4х4, будут образовывать дьявольский квадрат. Числа в четырех клетках, следующих последовательно одна за другой, как бы они ни были расположены – по вертикали, по горизонтали или по диагонали, – в сумме всегда дают постоянную квадрата. Современные математики называют подобные квадраты «совершенными».
ЛАТИНСКИЙ КВАДРАТ
Латинский квадрат – разновидность неправильных математических квадратов, заполненная n различными символами таким образом, чтобы в каждой строке и в каждом столбце встречались все n символов (каждый по одному разу).
Латинские квадраты существуют для любого n. Любой латинский квадрат является таблицей умножения (таблицей Кэли) квазигруппы. Название «латинский квадрат» берет начало от Леонарда Эйлера, который использовал латинские буквы вместо цифр в таблице.
Два латинских квадрата называются ортогональными , если различны все упорядоченные пары символов (a,b), где a – символ в некоторой клетке первого латинского квадрата, а b – символ в той же клетке второго латинского квадрата.
Ортогональные латинские квадраты существуют для любого порядка, кроме 2 и 6. Для n являющихся степенью простого числа есть набор n–1 попарно ортогональных латинских квадратов. Если в каждой диагонали латинского квадрата все элементы различны, такой латинский квадрат называется диагональным . Пары ортогональных диагональных латинских квадратов существуют для всех порядков, кроме 2, 3 и 6. Латинский квадрат часто встречается в задачах составления расписания, поскольку в строках и столбцах числа не повторяются.
Квадрат из пар элементов двух ортогональных латинских квадратов называется греко-латинский квадратом . Подобные квадраты часто используются для построения магических квадратов и в усложненных задачах о составлении расписания.
Занимаясь греко-латинскими квадратами Эйлер доказал, что квадратов второго порядка не существует, зато были найдены квадраты 3, 4, и 5 порядков. Ни одного квадрата 6 порядка он не нашел. Им была высказана гипотеза, что не существует квадратов четных порядков, не делящееся на 4 (то есть 6, 10, 14 и т. д.). В 1901 Гастон Терри перебором подтвердил гипотезу для 6 порядка. Но в 1959 году гипотеза была опровергнута Э. Т. Паркером, Р. К. Боусом и С. С. Шрикхердом, обнаружившими греко-латинский квадрат порядка 10.
ПОЛИМИНО АРТУРА КЛАРКА

Полимино – по сложности его, безусловно, относится к категории труднейших математических квадратов. Вот как о нем пишет писатель-фантаст А. Кларк – ниже размещен отрывок из книги "Земная Империя". Очевидно, что Кларк, проживая на своем острове, он жил на Цейлоне – и его философия отрыва от социума интересна сама по себе, увлекся развлечением, которому учит бабушка мальчика, и передал его нам. Предпочтем это живое описание имеющимся систематизациям, которые передают, возможно, суть, но не дух игры.
– Ты уже достаточно большой мальчик, Дункан, и сумеешь понять эту игру… впрочем, она куда больше, чем игра. Вопреки словам бабушки, игра не впечатлила Дункана. Ну что можно сделать из пяти белых пластмассовых квадратиков?
– Прежде всего,– продолжала бабушка,– тебе нужно проверить, сколько различных узоров ты сумеешь сложить из квадратиков.
– А они при этом должны лежать на столе? – спросил Дункан.
– Да, они должны лежать, соприкасаясь. Перекрывать один квадратик другим нельзя.
Дункан принялся раскладывать квадратики.
– Ну, я могу выложить их все в прямую линию,– начал он.– Вот так… А потом могу переложить две штуки и получить букву L… А если я возьмусь за другой край, то получится буква U…
Мальчик быстро составил полдюжины сочетаний, потом еще и вдруг обнаружил, что они повторяют уже имеющиеся.
– Может, я тупой, но это все.
Дункан упустил самую простую из фигур – крест, для создания которой достаточно было выложить четыре квадратика по сторонам пятого, центрального.
– Большинство людей начинают как раз с креста,– улыбнулась бабушка.– По-моему, ты поторопился объявить себя тупым. Лучше подумай: могут ли быть еще какие-нибудь фигуры?
Сосредоточенно двигая квадратики, Дункан нашел еще три фигуры, после чего прекратил поиски.
– Теперь уже точно все, – уверенно заявил он.
– А что ты скажешь про такую фигуру?
Слегка передвинув квадратики, бабушка сложила из них подобие горбатой буквы F.
– И вот еще одна.
Дункан чувствовал себя последним идиотом, и бабушкины слова легли бальзамом на его смущенную душу:
– Ты просто молодец. Подумаешь, упустил всего две фигуры. А общее число фигур равно двенадцати. Не больше и не меньше. Теперь ты знаешь их все. Ищи хоть целую вечность – больше не найдешь ни одной.
Бабушка смела в угол пять белых квадратиков и выложила на стол дюжину ярких разноцветных пластиковых кусочков. Это были те самые двенадцать фигур, но уже в готовом виде, и каждая состояла из пяти квадратиков. Дункан уже был готов согласиться, что никаких других фигур действительно не существует.
Но раз бабушка выложила эти разноцветные полоски, значит, игра продолжается, и Дункана ждал еще один сюрприз.
– А теперь, Дункан, слушай внимательно. Эти фигуры называются «пентамино». Название произошло от греческого слова «пента», что значит «пять». Все фигуры равны по площади, поскольку каждая состоит из пяти одинаковых квадратиков. Фигур двенадцать, квадратиков – пять, следовательно, общая площадь будет равняться шестидесяти квадратикам. Правильно?
– Мм…да.
– Слушай дальше. Шестьдесят – замечательное круглое число, которое можно составить несколькими способами. Самый легкий – умножить десять на шесть. Такую площадь имеет эта коробочка: по горизонтали в ней умещается десять квадратиков, а по вертикали – шесть. Стало быть, в ней должны уместиться все двенадцать фигур. Просто, как составная картинка-загадка.
Дункан ожидал подвоха. Бабушка обожала словесные и математические парадоксы, и далеко не все они были понятии ее десятилетней жертве. Но на сей раз обошлось без парадоксов. Дно коробки было расчерчено на шестьдесят квадратиков, значит… Стоп! Площадь площадью, но ведь фигуры имеют разные очертания. Попробуй-ка загони их в коробку!
– Оставляю тебе эту задачу для самостоятельного решения,– объявила бабушка, видя, как он уныло двигает пентамино по дну коробки.– Поверь мне, их можно собрать.
Вскоре Дункан начал крепко сомневаться в бабушкиных словах. Ему с легкостью удавалось уложить в коробку десять фигур, а один раз он ухитрился втиснуть и одиннадцатую. Но очертания незаполненного пространства не совпадали с очертаниями двенадцатой фигуры, которую мальчик вертел в руках. Там был крест, а оставшаяся фигура напоминала букву Z…
Еще через полчаса Дункан уже находился на грани отчаяния. Бабушка погрузилась в диалог со своим компьютером, но время от времени заинтересованно поглядывала на него, словно говоря: «Это не так легко, как ты думал».
В свои десять лет Дункан отличался заметным упрямством. Большинство его сверстников давным-давно оставили бы всякие попытки. (Только через несколько лет он понял, что бабушка изящно проводила с ним психологический тест.) Дункан продержался без посторонней помощи почти сорок минут…
Тогда бабушка встала от компьютера и склонилась над головоломкой. Ее пальцы передвинули фигуры U, X и L…
Дно коробки оказалось целиком заполненным! Все куски головоломки заняли нужные места.
– Конечно, ты заранее знала ответ! – обиженно протянул Дункан.
– Ответ? – переспросила бабушка.– А как ты думаешь, сколькими способами можно уложить пентамино в эту коробку?
Вот она, ловушка. Дункан провозился почти час, так и не найдя решения, хотя за это время он перепробовал не меньше сотни вариантов. Он думал, что существует всего один способ. А их может быть… двенадцать? Или больше?
– Так сколько, по-твоему, может быть способов? – снова спросила бабушка.
– Двадцать,– выпалил Дункан, думая, что уж теперь бабушка не будет возражать.
– Попробуй снова.
Дункан почуял опасность. Забава оказалась куда хитрее, чем он думал, и мальчик благоразумно решил не рисковать.
– Вообще-то, я не знаю,– сказал он, мотая головой.
– А ты восприимчивый мальчик,– снова улыбнулась бабушка.– Интуиция – опасный проводник, но порою другого у нас нет. Могу тебя обрадовать: угадать правильный ответ здесь невозможно. Существует более двух тысяч различных способов укладки пентамино в эту коробку. Точнее, две тысячи триста тридцать девять. И что ты на это скажешь?
Вряд ли бабушка его обманывала. Но Дункан был настолько раздавлен своей неспособностью найти решение, что не удержался и выпалил:
– Не верю!
Элен редко выказывала раздражение. Когда Дункан чем-то обижал ее, она просто становилась холодной и отрешенной. Однако сейчас бабушка лишь усмехнулась и что-то выстучала на клавиатуре компьютера.
– Взгляни сюда,– предложила она.
На экране появился набор из двенадцати разноцветных пентамино, заполняющих прямоугольник размером десять на шесть. Через несколько секунд его сменило другое изображение, где фигуры, скорее всего, располагались уже по-другому (точно сказать Дункан не мог, поскольку не запомнил первую комбинацию). Вскоре изображение опять поменялось, потом еще и еще… Так продолжалось, пока бабушка не остановила программу.
– Даже при большой скорости компьютеру понадобится пять часов, чтобы перебрать все способы,– пояснила бабушка.– Можешь поверить мне на слово: все они разные. Если бы не компьютеры, сомневаюсь, что люди нашли бы все способы обычным перебором вариантов.
Дункан долго глядел на двенадцать обманчиво простых фигур. Он медленно переваривал бабушкины слова. Это было первое в его жизни математическое откровение. То, что он так опрометчиво посчитал обыкновенной детской игрой, вдруг стало разворачивать перед ним бесконечные тропинки и горизонты, хотя даже самый одаренный десятилетний ребенок вряд ли сумел бы ощутить безграничность этой вселенной.
Но тогда восторг и благоговение Дункана были пассивными. Настоящий взрыв интеллектуального наслаждения случился позже, когда он самостоятельно отыскал свой первый способ укладки пентамино. Несколько недель Дункан везде таскал с собой пластмассовую коробочку. Все свободное время он тратил только на пентамино. Фигуры превратитесь в личных друзей Дункана. Он называл их по буквам, которые те напоминали, хотя в ряде случае сходство было более чем отдаленным. Пять фигур – F, I, L, Р, N шли вразнобой, зaто остальные семь повторяли последовательность латинского алфавита: Т, U, V, W, X, Y, Z.
Однажды, в состоянии не то геометрического транса, не то геометрического экстаза, который больше не повторялся, Дункан менее чем за час нашел пять вариантов укладки. Возможно, даже Ньютон, Эйнштейн или Чэнь-цзы в свои моменты истины не ощущали большего родства с богами математики, чем Дункан Макензи.
Вскоре он сообразил, причем сам, без бабушкиных подсказок, что пентамино можно уложить в прямоугольник с другими размерами сторон. Довольно легко Дункан нашел несколько вариантов для прямоугольников 5 на 12 и 4 на 15. Затем он целую неделю мучился, пытаясь загнать двенадцать фигур в более длинный и узкий прямоугольник 3 на 20. Снова и снова он начинал заполнять коварное пространство и… получат дыры в прямоугольнике и «лишние» фигуры.
Сокрушенный, Дункан наведался к бабушке, где его ждал новый сюрприз.
– Я рада твоим опытам,– сказала Элен.– Ты исследовал все возможности, пытаясь вывести общую закономерность. Так всегда поступают математики. Но ты ошибаешься: решения для прямоугольника три на двадцать все-таки существуют. Их всего два, и если ты найдешь одно, то сумеешь отыскать и второе.
Окрыленный бабушкиной похвалой, Дункан с новыми силами продолжил «охоту на пентамино». Еще через неделю он начал понимать, какой непосильный груз взвалил на свои плечи. Количество способов, которым можно расположить двенадцать фигур, просто ошеломляло Дункана. Более того, ведь каждая фигура имела четыре положения!
И вновь он явился к бабушке, выложив ей все свои затруднения. Если для прямоугольника 3 на 20 существовало только два варианта, сколько же времени понадобится, чтобы их найти?
– Изволь, я тебе отвечу,– сказала бабушка.– Если бы ты действовал как безмозглый компьютер, занимаясь простым перебором комбинаций и тратя на каждую по одной секунде, тебе понадобилось бы…– Здесь она намеренно сделала паузу.– Тебе понадобилось бы более шести миллионов… да, более шести миллионов лет.
Земных или титанских? Этот вопрос мгновенно возник в мозгу Дункана. Впрочем, какая разница?
– Но ты отличаешься от безмозглого компьютера,– продолжала бабушка.– Ты сразу видишь заведомо непригодные комбинации, и потому тебе не надо тратить время на их проверку. Попробуй еще раз.
Дункан повиновался, уже без энтузиазма и веры в успех. А потом ему в голову пришла блестящая идея.
Карл сразу же заинтересовался пентамино и принял вызов. Он взял у Дункана коробочку с фигурами и исчез на несколько часов.
Когда Карл позвонил ему, вид у друга был несколько расстроенный.
– А ты уверен, что эта задача действительно имеет решение? – спросил он.
– Абсолютно уверен. Их целых два. Неужели ты так и не нашел хотя бы одно? Я-то думал, ты здорово соображаешь в математике.
– Представь себе, соображаю, потому и знаю, каких трудов стоит твоя задачка. Нужно проверить… миллион миллиардов возможных комбинаций.
– А откуда ты узнал, что их столько? – спросил Дункан, довольный тем, что хоть чем-то сумел заставить друга растерянно чесать в затылке.
Карл скосил глаза на лист бумаги, заполненный какими-то схемами и цифрами.
– Если исключить недопустимые комбинации и учесть симметрию и возможность поворота… получается факториал… суммарное число перестановок… ты все равно не поймешь. Я тебе лучше покажу само число.
Он поднес к камере другой лист, на котором была крупно изображена внушительная вереница цифр:
1 004 539 160 000 000.
Дункан ничего не смыслил в факториалах, однако в точности подсчетов Карла не сомневался. Длиннющее число ему очень понравилось.
– Так ты собрался бросить эту задачу? – осторожно спросил Дункан.
– Еще чего! Я просто хотел тебе показать, насколько она трудна.
Лицо Карла выражало мрачную решимость. Произнеся эти слова, он отключился.
На следующий день Дункана ожидало одно из величайших потрясений в его мальчишеской жизни. С экрана на него смотрело осунувшееся, с воспаленными глазами, лицо Карла. Чувствовалось, он провел бессонную ночь.
– Ну вот и все,– усталым, но торжествующим голосом возвестил он.
Дункан едва верил своим глазам. Ему казалось, что шансы на успех ничтожно малы. Он даже убедил себя в этом. И вдруг… Перед ним лежал прямоугольник три на двадцать, заполненный всеми двенадцатью фигурами пентамино.
Потом Карл поменял местами и перевернул фигуры на концах, оставив центральную часть нетронутой. От усталости у него слегка дрожали пальцы.
– Это второе решение,– пояснил он.– А теперь я отправляюсь спать. Так что спокойной ночи или доброго утра – это уж как тебе угодно.
Посрамленный Дункан еще долго глядел в погасший экран. Он не знал, какими путями двигался Карл, нащупывая решение головоломки. Но он знал, что его друг вышел победителем. Наперекор всему.
Он не завидовал победе друга. Дункан слишком любил Карла и всегда радовался его успехам, хотя нередко сам оказывался побежденной стороной. Но в сегодняшнем триумфе друга было что-то иное, что-то почти магическое.
Дункан впервые увидел, какой силой обладает интуиция. Он столкнулся с загадочной способностью разума вырываться за пределы фактов и отбрасывать в сторону мешающую логику. За считаные часы Карл выполнил колоссальную работу, превзойдя самый быстродействующий компьютер.
Впоследствии Дункан узнал, что подобными способностями обладают все люди, но используют они их крайне редко – возможно, один раз в жизни. У Карла этот дар получил исключительное развитие… С того момента Дункан стал серьезно относиться к рассуждениям друга, даже самым нелепым и возмутительным с точки зрения здравого смысла.
Это было двадцать лет назад. Дункан не помнил, куда делись пластмассовые фигуры пентамино. Возможно, так и остались у Карла.
Бабушкин подарок стал их новым воплощением, теперь уже в виде кусочков разноцветного камня. Удивительный, нежно-розового оттенка гранит был с холмов Галилея, обсидиан – с плато Гюйгенса, а псевдомрамор – с гряды Гершеля. И среди них… сначала Дункан подумал, что ошибся. Нет, так оно и есть: то был самый редкий и загадочный минерал Титана. Крест каменного пентамино бабушка сделала из титанита. Этот иссиня-черный, с золотистыми вкраплениями минерал не спутаешь ни с чем. Таких крупных кусков Дункан еще не видел и мог только догадываться, какова его стоимость.
– Не знаю, что и сказать,– пробормотал он.– Какая красота. Такое я вижу в первый раз.
Он обнял худенькие бабушкины плечи и вдруг почувствовал, что они дрожат и ей никак не унять эту дрожь. Дункан бережно держал ее в своих объятиях, пока плечи не перестали дрожать. В такие мгновения слова не нужны. Отчетливее, чем прежде, Дункан понимал: он последняя любовь в опустошенной жизни Элен Макензи. И теперь он улетает, оставляя ее наедине с воспоминаниями.

БОЛЬШИЕ МАГИЧЕСКИЕ КВАДРАТЫ
Китайский математик XIII века Ян Хуэй был знаком с треугольником Паскаля (арифметическим треугольником). Он оставил изложение методов решения уравнений 4-й и высших степеней, встречаются правила решения полного квадратного уравнения, суммирования прогрессий, приемы построения магических квадратов. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37).
Бенджамин Франклин составил квадрат 16×16, который помимо наличия постоянной суммы 2056 во всех строках, столбцах и диагоналях имел еще одно дополнительное свойство. Если вырезать из листа бумаги квадрат 4×4 и уложить этот лист на большой квадрат так, чтобы 16 клеток большего квадрата попали в эту прорезь, то сумма чисел, появившихся в этой прорези, куда бы мы ее не положили, будет одна и та же – 2056.
Самым ценным в этом квадрате является то, что его довольно просто превратить в идеальный магический квадрат, в то время как построение идеальных магических квадратов – нелегкая задача. Франклин называл этот квадрат "самым очаровательным волшебством из всех магических квадратов, когда-либо сотворенных чародеями".
Маги́ческий , или волше́бный квадра́т - квадратная таблица n × n {\displaystyle n\times n} , заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим . Нормальным называется магический квадрат, заполненный натуральными числами от 1 {\displaystyle 1} до n 2 {\displaystyle n^{2}} . Магический квадрат называется ассоциативным или симметричным , если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n 2 + 1 {\displaystyle n^{2}+1} .
Нормальные магические квадраты существуют для всех порядков n ≥ 1 {\displaystyle n\geq 1} , за исключением n = 2 {\displaystyle n=2} , хотя случай n = 1 {\displaystyle n=1} тривиален - квадрат состоит из одного числа. Минимальный нетривиальный случай показан ниже, он имеет порядок 3.
| 2 | 7 | 6 | 15 | |||
| 9 | 5 | 1 | → {\displaystyle \rightarrow } | 15 | ||
| 4 | 3 | 8 | → {\displaystyle \rightarrow } | 15 | ||
| ↙ {\displaystyle \swarrow } | ↓ {\displaystyle \downarrow } | ↓ {\displaystyle \downarrow } | ↘ {\displaystyle \searrow } | |||
| 15 | 15 | 15 | 15 | 15 |
Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой, M . Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
M (n) = n (n 2 + 1) 2 {\displaystyle M(n)={\frac {n(n^{2}+1)}{2}}}Почему это так? |
|
|---|---|
Пусть имеется квадрат со стороной n . {\displaystyle n.} Тогда в нём будет n 2 {\displaystyle n^{2}} чисел. С одной стороны, сумма чисел S = 1 + 2 + 3 + … + n 2 = n 2 2 (n 2 + 1) . {\displaystyle S=1+2+3+\ldots +n^{2}={\cfrac {n^{2}}{2}}(n^{2}+1).} С другой стороны, S = n M . {\displaystyle S=nM.} Приравняв, получим искомую формулу. |
|
Первые значения магических констант приведены в следующей таблице (последовательность A006003 в OEIS):
| Порядок n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| M (n) | 15 | 34 | 65 | 111 | 175 | 260 | 369 | 505 | 671 | 870 | 1105 |
Энциклопедичный YouTube
1 / 5
✪ Магический квадрат - фокус для вечеринок
✪ Квадрат Паркера
✪ Страница 35 Задание на полях (первый квадрат) – Математика 3 класс Моро – Учебник Часть 1
✪ Магический квадрат - новый метод
✪ Магические квадраты. Открытое занятие.
Субтитры
Исторически значимые магические квадраты
Квадрат Ло Шу
Магический квадрат Ян Хуэя (Китай)
| 27 | 29 | 2 | 4 | 13 | 36 |
| 9 | 11 | 20 | 22 | 31 | 18 |
| 32 | 25 | 7 | 3 | 21 | 23 |
| 14 | 16 | 34 | 30 | 12 | 5 |
| 28 | 6 | 15 | 17 | 26 | 19 |
| 1 | 24 | 33 | 35 | 8 | 10 |
Квадрат Альбрехта Дюрера
Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I », считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания гравюры ().
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+12+15+5 и 3+8+14+9), в вершинах прямоугольников, параллельных диагоналям (2+8+15+9 и 3+12+14+5), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.
Если в квадратную матрицу n × n заносится не строго натуральный ряд чисел, то данный магический квадрат - нетрадиционный . Ниже представлены два таких магических квадрата, заполненные простыми числами (хотя 1 в современной теории чисел не считается простым числом). Первый имеет порядок n=3 (квадрат Дьюдени); второй (размером 4x4 ) - квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия :
|
|
Есть еще несколько подобных примеров:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
| 1 | 823 | 821 | 809 | 811 | 797 | 19 | 29 | 313 | 31 | 23 | 37 |
| 89 | 83 | 211 | 79 | 641 | 631 | 619 | 709 | 617 | 53 | 43 | 739 |
| 97 | 227 | 103 | 107 | 193 | 557 | 719 | 727 | 607 | 139 | 757 | 281 |
| 223 | 653 | 499 | 197 | 109 | 113 | 563 | 479 | 173 | 761 | 587 | 157 |
| 367 | 379 | 521 | 383 | 241 | 467 | 257 | 263 | 269 | 167 | 601 | 599 |
| 349 | 359 | 353 | 647 | 389 | 331 | 317 | 311 | 409 | 307 | 293 | 449 |
| 503 | 523 | 233 | 337 | 547 | 397 | 421 | 17 | 401 | 271 | 431 | 433 |
| 229 | 491 | 373 | 487 | 461 | 251 | 443 | 463 | 137 | 439 | 457 | 283 |
| 509 | 199 | 73 | 541 | 347 | 191 | 181 | 569 | 577 | 571 | 163 | 593 |
| 661 | 101 | 643 | 239 | 691 | 701 | 127 | 131 | 179 | 613 | 277 | 151 |
| 659 | 673 | 677 | 683 | 71 | 67 | 61 | 47 | 59 | 743 | 733 | 41 |
| 827 | 3 | 7 | 5 | 13 | 11 | 787 | 769 | 773 | 419 | 149 | 751 |
Последний квадрат, построенный в 1913 г. Дж. Н. Манси примечателен тем, что он составлен из 143 последовательных простых чисел за исключением двух моментов: привлечена единица, которая не является простым числом, и не использовано единственное чётное простое число 2.
Квадраты с дополнительными свойствами
Дьявольский магический квадрат
Дьявольский квадрат или пандиагональный квадрат - магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.
Существует 48 дьявольских квадратов 4×4 с точностью до поворотов и отражений. Если принять во внимание ещё и симметрию относительно торических параллельных переносов , то остаётся только 3 существенно различных квадрата:
|
|
|
Пандиагональные квадраты существуют для нечётного порядка n>3, для любого порядка двойной чётности n=4k (k=1,2,3…) и не существуют для порядка одинарной чётности n = 4 k + 2 {\displaystyle n=4k+2} ( k = 1 , 2 , 3 , … {\displaystyle k=1,2,3,\dots } ).
Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными . Совершенных квадратов нечётного порядка не существует. Среди пандиагональных квадратов двойной чётности выше 4 имеются совершенные.
Пандиагональных квадратов пятого порядка 3600. С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов. Один из них показан ниже.
| 1 | 15 | 24 | 8 | 17 |
| 9 | 18 | 2 | 11 | 25 |
| 12 | 21 | 10 | 19 | 3 |
| 20 | 4 | 13 | 22 | 6 |
| 23 | 7 | 16 | 5 | 14 |
Если пандиагональный квадрат еще и ассоциативный, то он носит название идеальный . Пример идеального магического квадрата:
| 21 | 32 | 70 | 26 | 28 | 69 | 22 | 36 | 65 |
| 40 | 81 | 2 | 39 | 77 | 7 | 44 | 73 | 6 |
| 62 | 10 | 51 | 58 | 18 | 47 | 57 | 14 | 52 |
| 66 | 23 | 34 | 71 | 19 | 33 | 67 | 27 | 29 |
| 4 | 45 | 74 | 3 | 41 | 79 | 8 | 37 | 78 |
| 53 | 55 | 15 | 49 | 63 | 11 | 48 | 59 | 16 |
| 30 | 68 | 25 | 35 | 64 | 24 | 31 | 72 | 20 |
| 76 | 9 | 38 | 75 | 5 | 43 | 80 | 1 | 42 |
| 17 | 46 | 60 | 13 | 54 | 56 | 12 | 50 | 61 |
Известно, что не существует идеальных магических квадратов порядка n = 4k+2 и квадрата порядка n = 4 . В то же время, существуют идеальные квадраты порядка n = 8 . Методом построения составных квадратов можно построить на базе данного квадрата восьмого порядка идеальные квадраты порядка n = 8k, k=5,7,9… и порядка n = 8^p, p=2,3,4… В 2008 г. разработан комбинаторный метод построения идеальных квадратов порядка n = 4k, k = 2, 3, 4,…
Построение магических квадратов
Метод террас
Описан Ю. В. Чебраковым в «Теории магических матриц» .
Для заданного нечетного n начертим квадратную таблицу размером n на n. Пристроим к этой таблице со всех четырех сторон террасы (пирамидки). В результате получим ступенчатую симметричную фигуру.
|
Начиная с левой вершины ступенчатой фигуры, заполним её диагональные ряды последовательными натуральными числами от 1 до N 2 {\displaystyle N^{2}} .
После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером NxN, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.
|
|
Кроме того, данный способ является верным и в том случае, если магический квадрат нужно составить не из чисел от 1 до N, но и от K до N, где 1 <= K< N.
Прочие способы
Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы. Найти все магические квадраты порядка n {\displaystyle n} удается только для n ≤ 4 {\displaystyle n\leq 4} , поэтому представляют большой интерес частные процедуры построения магических квадратов при n > 4 {\displaystyle n>4} . Проще всего конструкция для магического квадрата нечетного порядка. Нужно в клетку с координатами (i , j) {\displaystyle (i,j)} (где i {\displaystyle i} и j {\displaystyle j} меняются от 1 до n {\displaystyle n} ) поставить число
1 + ((i + j − 1 + (n − 1) / 2) mod n) n + ((i + 2 j + 2) mod n) . {\displaystyle 1+((i+j-1+(n-1)/2){\bmod {n}})n+((i+2j+2){\bmod {n}}).} [ ]Ещё проще построение выполнить следующим образом. Берётся матрица n x n . Внутри её строится ступенчатый ромб. В нём ячейки слева вверх по диагоналям заполняются последовательным рядом нечётных чисел. Определяется значение центральной ячейки C. Тогда в углах магического квадрата значения будут такими: верхняя правая ячейка C-1 ; нижня левая ячейка C+1 ; нижняя правая ячейка C-n; верхняя левая ячейка C+n. Заполнение пустых ячеек в ступенчатых угловых треугольниках ведётся с соблюдением простых правил: 1)по строкам числа слева направо увеличиваются с шагом n + 1; 2) по столбцам сверху вниз числа увеличиваются с шагом n-1.
Также разработаны алгоритмы построения пандиагональных квадратов, и идеальных магических квадратов 9x9. Эти результаты позволяют строить идеальные магические квадраты порядков n = 9 (2 k + 1) {\displaystyle n=9(2k+1)} для k = 0 , 1 , 2 , 3 , … {\displaystyle k=0,1,2,3,\dots } . Существуют также общие методы компоновки идеальных магических квадратов нечётного порядка n > 3 {\displaystyle n>3} . Разработаны методы построения идеальных магических квадратов порядка n=8k, k=1,2,3… и совершенных магических квадратов. Пандиагональные и идеальные квадраты четно-нечётного порядка удаётся скомпоновать лишь в том случае, если они нетрадиционные. Тем не менее, можно находить почти пандиагональные квадраты Найдена особая группа идеально-совершенных магических квадратов (традиционных и нетрадиционных) .
Примеры более сложных квадратов
Методически строго отработаны магические квадраты нечётного порядка и порядка двойной чётности. Формализация квадратов порядка одинарной чётности намного труднее, что иллюстрируют следующие схемы:
|
|
|
Существуют несколько десятков других методов построения магических квадратов
Секрет игры «Магический квадрат»
Уверена, вы где-то слышали такое словосочетание, как «магический квадрат». Нам известны несколько представителей этого «племени». Самый распространённый и часто встречающийся в интернете - это так называемая игра «Магический квадрат». Суть её заключается в том, что вашему вниманию предлагается таблица (это и есть «магический квадрат»), которая способна «угадывать мысли». Естественно, что, как и у любой игры, у нее есть определённые правила. Необходимо задумать любое двузначное число, а затем вычесть из него сумму, состоящую из цифр этого числа. Отыскать полученное значение в таблице вместе с символом, ему соответствующим. И как раз этот символ и отгадывает квадрат. Игра забавная и, на первый взгляд, действительно магическая, потому что какое бы число вы не загадывали первоначально - квадрат всегда угадывает символ. Как это получается? Как работает «магический квадрат»? На самом деле ответ лежит на поверхности. Если проверять квадрат несколько раз подряд, то можно заметить, что все время выпадает один и тот же символ. При более внимательном рассмотрении таблицы видно, что этот символ расположен по горизонтали и ему соответствуют цифры, без остатка делящиеся на 9. Впрочем, только они и получаются в вашем ответе, какое бы двузначное число вы не выбрали. Можно сказать, что мы разоблачили «магический квадрат». Секрет заключается не столько в нем, сколько в условиях игры. Дело в том, что есть такая неоспоримая истина, которая гласит: «Если из любого двузначного числа вычесть сумму его цифр, получится число, без остатка делящееся на 9». Вот мы и выяснили, как работает «магический квадрат». Ни грамма мистики! Хотя в принципе, все, что связанно с цифрами, основано на вычислениях и закономерностях, а никак не на волшебстве.
Секрет магического квадрата:
| 7 | t | 41 | k | 86 | h | 21 | n | 33 | w | 1 | p | 35 | r | 61 | p | 12 | w | 90 | a |
| 15 | h | 23 | z | 57 | v | 55 | q | 71 | d | 66 | h | 78 | g | 14 | q | 81 | a | 10 | t |
| 88 | d | 59 | j | 74 | n | 69 | b | 68 | m | 38 | i | 22 | m | 72 | a | 3 | v | 58 | m |
| 62 | l | 77 | m | 40 | c | 98 | u | 20 | s | 94 | m | 63 | a | 87 | t | 99 | m | 37 | x |
| 92 | s | 96 | g | 51 | f | 73 | e | 46 | i | 54 | a | 53 | s | 44 | h | 43 | k | 2 | d |
| 34 | o | 31 | e | 91 | t | 19 | i | 45 | a | 50 | k | 85 | v | 28 | s | 38 | l | 75 | v |
| 79 | h | 8 | c | 11 | s | 36 | a | 16 | f | 24 | z | 4 | q | 67 | m | 6 | f | 48 | o |
| 17 | p | 65 | w | 27 | a | 42 | p | 89 | e | 39 | s | 95 | x | 32 | f | 25 | d | 26 | h |
| 29 | c | 18 | a | 82 | k | 60 | o | 93 | r | 83 | y | 52 | k | 56 | p | 53 | i | 30 | y |
| 9 | a | 80 | q | 47 | d | 84 | l | 5 | g | 13 | x | 70 | d | 49 | g | 76 | c | 64 | e |
Магический квадрат Альбрехта Дюрера
Иногда цифровые закономерности приобретают такие невероятные масштабы, что, кажется, без колдовства здесь не обошлось. Так, например, известен ещё один «магический квадрат» - Альбрехта Дюрера. В математике под ним понимают квадратную таблицу с одинаковым количеством строк и столбцов, заполненную натуральными числами. Причём, сумма этих чисел по горизонтали, вертикали или диагонали должна равняться одному и тому же результату. Магический квадрат пришёл к нам из Китая, сегодня мы все знаем его яркого представителя - кроссворд «Судоку». В Европе первым «волшебную» фигуру изобразил именно Дюрер на своей гравюре «Меланхолия». В чем же уникальность этого «магического квадрата»? В своём основании он имеет сочетание цифр 15 и 14, что соответствует году издания гравюры. А сумма цифр складывается не только из строк по диагонали, вертикали и горизонтали, но и из цифр, стоящих по углам квадрата, в центральном маленьком квадрате и в каждом из четырёхклеточных квадратов по его сторонам. Эти фигуры не предсказывают судьбу и не угадывают мысли, они уникальны именно своими закономерностями.

Квадрат Пифагора
Если же обратиться к гаданиям, то и здесь есть свой представитель - «магический квадрат» Пифагора. Всем нам известно такое имя из уроков геометрии. Но только в наше время этого человека начали называть математиком и философом. В древности же он был известен как учитель мудрости, о нем слагались стихи и пелись оды, ему поклонялись, считали провидцем. Пифагор основал новую науку - нумерологию, в прежние времена она воспринималась как религия.

Он считал, что цифры могут объяснить практически каждое явление, в том числе и определить судьбу человека, рассказать о его характере, талантах и слабостях. Это можно было сделать при помощи квадрата Пифагора. Как работает «магический квадрат» и что из себя представляет? Магический квадрат Пифагора - это квадрат 3/3 (строки, столбцы), в который внесены цифры от 1 до 9. За основу предсказания берётся дата рождения человека. Важно, что «0» в расчётах не фигурирует. С помощью нехитрых вычислений и формул получается набор цифр, который впоследствии необходимо вписать в квадрат. Каждое число имеет своё значение и отвечает за определённое свойство. Так, 4 «отвечает» за здоровье, а 9 - за ум. В зависимости от того, сколько раз в вашем квадрате встречается одна и та же цифра, можно сказать о преобладании того или иного свойства. Так, например, отсутствие 4 - показатель физической слабости и болезненности, а 444 - богатырское здоровье и жизнерадостность. Насколько правдив квадрат Пифагора, сложно сказать, как, впрочем, и любое гадание. Зато теперь, зная, как работает магический квадрат, вы, как минимум, сможете приятно скоротать часок-другой, рассчитывая характеры своих друзей и знакомых.
Данная загадка быстро разлетелась по всему Интернету. Тысячи людей начали задаваться вопросом о том, как работает магический квадрат. Сегодня вы, наконец-то, найдете ответ!
Тайна магического квадрата
На самом деле данная загадка довольно проста и сделана с расчётом на человеческую невнимательность. Давайте разберемся, как работает магический черный квадрат, на реальном примере:
- Давайте загадаем любое число от 10 до 19. Теперь давайте вычтем из данного числа его составляющие цифры. К примеру, возьмем 11. Отнимем от 11 единицу и после – еще одну единицу. Выйдет 9. На самом деле не важно, какое число от 10 до 19 вы возьмете. Результат вычислений всегда будет 9. Числу 9 в «Магическом Квадрате» соответствует первая цифра с рисунками. Если присмотреться, то можно увидеть, что очень большому количеству цифр присвоены одни и те же рисунки.
- Что же будет, если взять число в пределах от 20 и до 29? Может, вы уже сами догадались? Правильно! Результатом вычислений всегда будет 18. Цифра 18 соответствует второй позиции на диагонали с рисунками.
- Если же взять число от 30 до 39, то, как можно уже угадать, выйдет число 27. Число 27 также соответствует цифре на диагонали столь необъяснимого «Магического Квадрата».
- Подобный алгоритм остается правдивым для любых чисел от 40 до 49, от 50 до 59 и так далее.
То есть выходит, что неважно, какое число вы загадали - «Магический Квадрат» угадает результат, ведь в клетках под номерами 9, 18, 27, 36, 45, 54, 63, 72 и 81 на самом деле находится один и тот же символ.
На самом деле данную загадку можно легко объяснить с помощью простого уравнения:
- Вообразите любое двухзначное число. В независимости от числа его можно представить в виде x*10+y. Десятки выступают в роли “x”, а единицы в роли “у”.
- Вычтите из загаданного числа цифры, которые составляют его. Складываем уравнение: (x*10+y)-(x+y)=9*x.
- Число, которое вышло в результате вычислений должно указывать на определенный символ в таблице.
Не важно, какая цифра будет в роли “x”, так или иначе вы получите символ, у которого номер будет кратный девяти. Для того чтобы убедится в том, что под разными номерами находится один символ, достаточно просто посмотреть на таблицу и на номера 0,9,18,27,45,54,63,72,81 и последующие.